Оценка в Lp-нормах решения задач линейного программирования с приближенными данными
Чувенков А.Ф.1![]() , Рутта Н.А.1
, Рутта Н.А.1![]() , Стрюков М.Б.1
, Стрюков М.Б.1![]() , Болгова А.Э.1
, Болгова А.Э.1
1 Ростовский государственный экономический университет (РИНХ), Россия, Ростов-на-Дону
Скачать PDF | Загрузок: 25
Статья в журнале
Информатизация в цифровой экономике (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Том 4, Номер 1 (Январь-март 2023)
Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=52264050
Аннотация:
В статье рассматривается обусловленность решения корректных вычислительных задач линейного программирования (ЗЛП), заданных в канонической форме с неточно известными элементами матрицы и вектором данных. Дается в различных Lp-нормах оценка решения ЗЛП. Приводятся в виде теорем оценки погрешности решения ЗЛП с приближенно заданной правой частью, с приближенно заданной матрицей коэффициентов. Также в виде теорем получены оценки относительной погрешности обратной матрицы возмущений и абсолютной и относительной погрешностей приближенного решения ЗЛП в общем случае с приближенно заданными коэффициентами системы ограничений. Реализация разработанных авторами утверждений в виде ряда приведенных теорем позволяет эффективно проводить исследования бизнес-процессов в цифровой экономике на основе линейных математических моделей и более обоснованно получать решения вычислительных задач при работе с приближенными данными.
Введение
Актуальность выбранной темы обусловлена распространением и использованием мощных компьютеров и пакетов прикладных программ, возникновением массовой потребности быстро получать необходимые оценки и расчеты, не углубляясь в вычислительные детали и математические доказательства. Однако, бездумные вычисления могут приводить к очень большим ошибкам, если используются приближенные данные или необоснованные методы решения. Отсюда возникает целесообразность разработки этой темы и доведения результатов до потребителя.
Использование компьютеров для исследования каких-либо процессов или объектов в экономике опирается на соответствующие им математические модели с последующей формулировкой вычислительной задачи, выбором метода решения, счета по программе, обработке и интерпретации результатов. Из них самые распространенные в экономике модели оптимизации – задачи линейного программирования, которые и становятся нашей целью и задачей исследования.
Изученность проблемы достаточно полно представлена для систем линейных алгебраических уравнений с приближенными коэффициентами в работах [1-4] и линейных операторов, «возмущения» которых изучались в нормированных пространствах общего вида [5].
Целесообразность представленной темы и ее научной разработки определяется высокой практической значимостью получаемых результатов. Знакомство потребителей, работающих в сфере экономики с математическими моделями, с результатами исследования позволит им значительно улучшить обоснованность выводов при проведении вычислений с приближенными данными.
Научная новизна заключается в том, что исследования проведены в n-мерном пространстве с различными Lp-нормами для задач линейного программирования (ЗЛП) в общем виде, что важно при практическом применении.ЗЛП в математической форме имеет вид:
![]() (1)
(1)
![]()
где ![]() –неотрицательный вектор-столбец искомых
переменных
–неотрицательный вектор-столбец искомых
переменных ![]() ;
; ![]() – матрица известных коэффициентов размера
– матрица известных коэффициентов размера
![]() – вектор известных данных
– вектор известных данных ![]() ;
; ![]() – заданная линейная целевая функция
(см. [7-12]).
– заданная линейная целевая функция
(см. [7-12]).
Трудность решения вычислительной
задачи линейного программирования определяется тем, что как элементы матрицы ![]() , так и вектор данных
, так и вектор данных ![]() на практике известны неточно, с
определенной погрешностью. В некоторых случаях, определяемых структурой
матрицы, это может настолько сильно исказить оптимальное решение
на практике известны неточно, с
определенной погрешностью. В некоторых случаях, определяемых структурой
матрицы, это может настолько сильно исказить оптимальное решение ![]() , что его нельзя будет принять за ответ
и использовать в практической деятельности. Такие задачи относят к классу плохо
обусловленных вычислительных задач в отличие от некорректных задач,
рассмотренных в [13], которые после проведения регуляризации становятся
корректными. Считаем, что для каждого n-мерного вектора
, что его нельзя будет принять за ответ
и использовать в практической деятельности. Такие задачи относят к классу плохо
обусловленных вычислительных задач в отличие от некорректных задач,
рассмотренных в [13], которые после проведения регуляризации становятся
корректными. Считаем, что для каждого n-мерного вектора ![]()
![]() определена и фиксирована для
вещественного числа р,
определена и фиксирована для
вещественного числа р, ![]() , Lp-норма
, Lp-норма 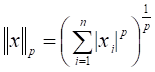 .Такие
пространства мы обозначаем
.Такие
пространства мы обозначаем ![]() , это полные
нормированные пространства (банаховы) [14,15]. Наиболее употребительными
являются следующие три пространства, определяемые нормами:
, это полные
нормированные пространства (банаховы) [14,15]. Наиболее употребительными
являются следующие три пространства, определяемые нормами:
![]() , выбор нормы
, выбор нормы ![]() определяется
случаем, когда учитывается суммарная абсолютная величина координат вектора;
определяется
случаем, когда учитывается суммарная абсолютная величина координат вектора; 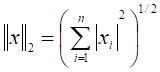 - евклидова норма;
- евклидова норма;
![]() ,
выбор нормы
,
выбор нормы ![]() означает,
что учитывается максимальная абсолютная компонента вектора.
означает,
что учитывается максимальная абсолютная компонента вектора.
Большинство вычислительных задач в
математике может быть записано в виде y = А(x), где А – некоторое преобразование,
действующее из нормированного пространства ![]() в нормированное пространство
в нормированное пространство
![]() . Для
оценки величин погрешностей приближения
. Для
оценки величин погрешностей приближения ![]() к входному
данному х и приближенного решения
к входному
данному х и приближенного решения ![]() к точному у
введены некоторые их меры: абсолютные погрешности
к точному у
введены некоторые их меры: абсолютные погрешности ![]() (используется
норма пространства
(используется
норма пространства ![]() ),
),
![]() (используется
норма пространства
(используется
норма пространства ![]() )
и относительные погрешности
)
и относительные погрешности 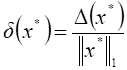 ,
, 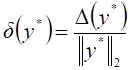 .
.
Предполагаем, что вычислительная
задача корректна, а именно: 1) для определенного множества допустимых
входных данных х из ![]() решение у из
пространства
решение у из
пространства ![]() существует;
2) единственно; 3) устойчиво. Наличие устойчивости означает, что
решение у может быть приближено последовательностью элементов
существует;
2) единственно; 3) устойчиво. Наличие устойчивости означает, что
решение у может быть приближено последовательностью элементов ![]() с любой точностью.
На практике конечные погрешности входных данных могут настолько сильно исказить
результат, что его нельзя будет принять за приближение точного решения.
с любой точностью.
На практике конечные погрешности входных данных могут настолько сильно исказить
результат, что его нельзя будет принять за приближение точного решения.
Если между абсолютными погрешностями
входных данных ![]() и
решения
и
решения ![]() вычислительной
задачи установлено неравенство
вычислительной
задачи установлено неравенство ![]() , то величина
, то величина ![]() называется абсолютным
коэффициентом обусловленности; в частности, величина
называется абсолютным
коэффициентом обусловленности; в частности, величина ![]() называется абсолютным числом
обусловленности; здесь
называется абсолютным числом
обусловленности; здесь ![]() нормы обратной
нормы обратной ![]() матриц (см. [3]).Если установлено
неравенство
матриц (см. [3]).Если установлено
неравенство ![]() между
относительными погрешностями данных и решения, то величину nd называют относительным коэффициентом
обусловленности.
между
относительными погрешностями данных и решения, то величину nd называют относительным коэффициентом
обусловленности.
Вычислительную задачу ![]() А(х)
называют хорошо обусловленной, если погрешностям входных данных отвечают
погрешности решения, обеспечивающие принятие нами приближенного решения с требуемой
точностью, и плохо обусловленной, если возможные погрешности настолько
искажают приближенное решение у*, что его нельзя принять за
решение задачи с заданной точностью (см. [4], [16-19].
А(х)
называют хорошо обусловленной, если погрешностям входных данных отвечают
погрешности решения, обеспечивающие принятие нами приближенного решения с требуемой
точностью, и плохо обусловленной, если возможные погрешности настолько
искажают приближенное решение у*, что его нельзя принять за
решение задачи с заданной точностью (см. [4], [16-19].
Приведем пример плохо обусловленной ЗЛП:


![]() ,
,
![]() ,
,
![]() ;
;
![]() ;
;
Здесь имеем ![]() в норме
в норме ![]() , точное решение
, точное решение ![]() ,
, ![]() Заменяя коэффициент 1 при
Заменяя коэффициент 1 при ![]() в первом уравнении системы
приближенным числом
в первом уравнении системы
приближенным числом ![]() , будем иметь для такой измененной
системы (
, будем иметь для такой измененной
системы ( ![]() ) решение
) решение ![]() ,
, ![]() которое свидетельствует о плохой
обусловленности ЗЛП.
которое свидетельствует о плохой
обусловленности ЗЛП.
Если изменить вектор данных в первоначальной
системе, уменьшив вторую координату на 1, получим ЗЛП ![]() ), для которой оптимальное решение
), для которой оптимальное решение ![]() ;
; ![]() . Опять имеем плохо обусловленную
задачу.
. Опять имеем плохо обусловленную
задачу.
Цель научного исследования состоит в получении оценок решения ЗЛП с приближенными данными, которые позволяют установить при каких ограничениях на погрешности приближенных данных вычислительная задача в определенных Lp-нормах будет хорошо обусловленной и приближенное решение может быть принято за конечный результат.
Теоретическая значимость исследования заключается в том, что полученные в ней результаты могу быть использованы не только для линейных задач оптимизации, но и в других линейных моделях микроэкономики и макроэкономики или эконометрики, применяемых в экономике, с известными приближенно данными.
Практическая значимость полученных результатов состоит в том, что ими может воспользоваться массовый потребитель, применяющий для исследования процессов или объектов в экономике линейные математические модели.
Методология исследования проблемы обусловленности вычислительных задач линейного программирования с приближенно известными данными заключалась в последовательной постановке в начале менее сложной задачи, ее решению, и переходе к решению более сложных задач. Для решения поставленных задач использовались методы линейной алгебры ( [3], [5], [12], [20-22]), исследования операций [6-11], вычислительной математики ( [4], [16-19]) и функционального анализа [14, 15].
1. оценка погрешности решения Злп с приближенно заданной правой частью
Предполагаем, что ЗЛП приведена к канонической форме
![]() ,
,
![]()
и известна невырожденная
матрица ![]() (считаем ранг
(считаем ранг ![]() ) при оптимальном базисном решении
) при оптимальном базисном решении ![]() (см. [4], [6], [8], [10]).
Рассматриваем случай, когда приближенно заданы исходные данные, вектор-столбец
(см. [4], [6], [8], [10]).
Рассматриваем случай, когда приближенно заданы исходные данные, вектор-столбец ![]() а элементы матрицы
а элементы матрицы ![]() системы уравнений
системы уравнений ![]() известны точно.
известны точно.
Теорема 1.Пусть ![]() точное решение системы
точное решение системы ![]() , в которой правая часть
, в которой правая часть ![]() есть приближение к
есть приближение к ![]() , с известными погрешностями:
абсолютной
, с известными погрешностями:
абсолютной ![]() и относительной
и относительной ![]() .Справедливы следующие утверждения:
.Справедливы следующие утверждения:
1) Для точного конкретного решения ![]() системы
системы ![]() верны следующие оценки абсолютной и
относительной погрешностей приближения
верны следующие оценки абсолютной и
относительной погрешностей приближения ![]() к
к ![]() :
:
![]()
![]()
2) Для любого решения ![]() системы
системы ![]() справедлива оценка
справедлива оценка
![]()
3)Справедлива оценка погрешности
значений целевой функции: ![]() где показатель q определяется из формулы
где показатель q определяется из формулы ![]()
Оценку 1) получаем из последовательности следующих преобразований:
![]()
![]()
Оценку относительной погрешности решения в пункте 2)получаем из неравенств:
![]()
![]()
Обозначаем через ![]() решение системы
решение системы ![]() в которой правая часть
в которой правая часть ![]() есть приближение к
есть приближение к ![]() , тогда
, тогда ![]() где
где ![]() неотрицательный ортант. Пусть
неотрицательный ортант. Пусть ![]() решение системы
решение системы ![]() и
и ![]() Используя неравенство Минковского (см.
[14, 15]), получаем оценку абсолютной погрешности 3) значений целевой функции
Используя неравенство Минковского (см.
[14, 15]), получаем оценку абсолютной погрешности 3) значений целевой функции
![]() где
где ![]() .
.
2. оценка погрешности решения Злп с приближенно заданной матрицей
Сохраняя обозначения предыдущего пункта
1, рассматриваем случай невырожденной матрицы ![]() с приближенно заданными
коэффициентами.
с приближенно заданными
коэффициентами.
Теорема 2. (Достаточное условие не вырождения
матрицы ![]() ).
).
Если абсолютная погрешность матрицы ![]() удовлетворяет ограничению
удовлетворяет ограничению
![]() ,
,
то матрица ![]() является невырожденной.
является невырожденной.
Обозначая через ![]() матрицу погрешностей, получаем равенство
матрицу погрешностей, получаем равенство
![]()
Отсюда следует, что матрица ![]() невырожденная тогда и только тогда,
когда невырожденная матрица
невырожденная тогда и только тогда,
когда невырожденная матрица ![]() . Из [3, 5] известно, что если
. Из [3, 5] известно, что если ![]() то это верно. Это справедливо и
когда
то это верно. Это справедливо и
когда ![]()
Отсюда получаем оценку ![]() , что и требовалось установить. Отметим,
что если матрица
, что и требовалось установить. Отметим,
что если матрица ![]() вырожденная, то
вырожденная, то ![]()
Достаточное условие не вырождения
матрицы ![]() через относительную погрешность
приближенного решения
через относительную погрешность
приближенного решения ![]() имеет вид
имеет вид ![]() .
.
Теорема 3. Пусть ![]() и
и ![]() есть решения систем
есть решения систем ![]() и
и ![]() , причем
, причем ![]() - невырожденная матрица.
Если
- невырожденная матрица.
Если ![]() то справедливы следующие оценки
абсолютной и относительной погрешностей приближенного решения
то справедливы следующие оценки
абсолютной и относительной погрешностей приближенного решения ![]() :
: ![]() ,
, ![]() .
.
В силу теоремы 2 матрица ![]() невырожденная и имеет обратную
невырожденная и имеет обратную ![]() тогда получаем следующую цепочку
неравенств:
тогда получаем следующую цепочку
неравенств:
![]()
![]()
![]()
Отсюда имеем искомую оценку
![]()
3. ОЦЕНКА погрешностиРЕШЕНИЯ ЗЛП В ОБЩЕМ СЛУЧАЕ с приближенно ЗАДАННЫМИКОЭФФИЦИЕНТАМИ СИСТЕМЫ ОГРАНИЧЕНИЙ И ПРАВОЙ ЧАСТЬЮ
Предполагаем, что ЗЛП приведена к канонической форме
![]() ,
,
![]()
и известна невырожденная
матрица ![]() (ранг
(ранг ![]() ) при оптимальном базисном решении
) при оптимальном базисном решении ![]() (см. [4], [6], [8], [10]).
Рассматриваем случай, когда приближенно заданы исходные данные, вектор-столбец
(см. [4], [6], [8], [10]).
Рассматриваем случай, когда приближенно заданы исходные данные, вектор-столбец ![]() и элементы матрицы
и элементы матрицы ![]() . Пусть А – невырожденная
матрица,
. Пусть А – невырожденная
матрица, ![]() - возмущенная матрица, то есть
- возмущенная матрица, то есть ![]() , где
, где ![]() - произвольная матрица возмущения.
- произвольная матрица возмущения.
При выполнении указанного в теореме 2
достаточного условия матрица ![]() невырожденная, поэтому справедливы
равенства:
невырожденная, поэтому справедливы
равенства:
![]()
= ![]()
и оценка (используется неравенство 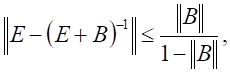 верное при
верное при ![]() ):
):
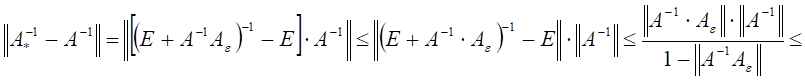
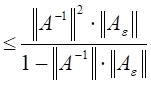 . Отсюда получаем следующую оценку
относительной погрешности матрицы возмущений
. Отсюда получаем следующую оценку
относительной погрешности матрицы возмущений ![]() :
:
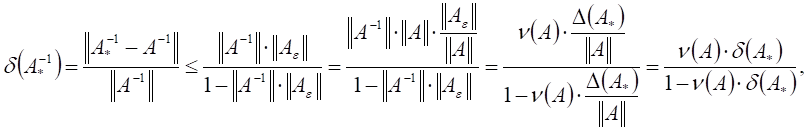 где
где ![]() есть число обусловленности матрицы
есть число обусловленности матрицы ![]() . Итак, справедлива
. Итак, справедлива
Теорема 4. При малом относительном возмущении
матрицы А: 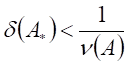 (или
(или ![]() ) и не слишком большом числе
обусловленности
) и не слишком большом числе
обусловленности ![]() матрицы
матрицы ![]() относительная погрешность обратной
матрицы возмущений
относительная погрешность обратной
матрицы возмущений ![]() будет мала:
будет мала: 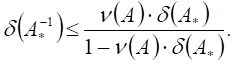
Предположим, что при указанных
условиях решаются уравнение ![]() , где
, где ![]() - невырожденная матрица, и
возмущенное уравнение
- невырожденная матрица, и
возмущенное уравнение ![]() Эти уравнения будут иметь
единственные решения
Эти уравнения будут иметь
единственные решения ![]() и
и ![]() . Обозначая относительные погрешности
возмущений через
. Обозначая относительные погрешности
возмущений через 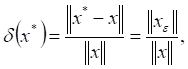
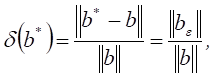 получаем следующие оценки:
получаем следующие оценки:
![]()
![]()
![]()
![]()
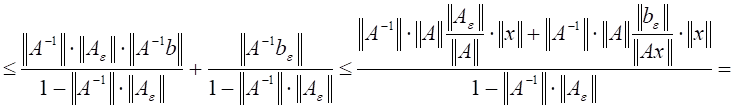
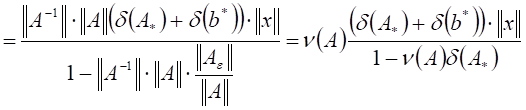 .
.
Это означает, что верна окончательная оценка
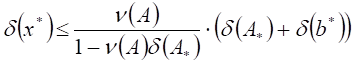 .
.
В полученной формуле важно, чтобы
коэффициент обусловленности 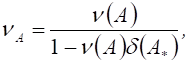 а также число обусловленности
а также число обусловленности ![]() матрицы А, были не слишком
большими. В частности, имеем
матрицы А, были не слишком
большими. В частности, имеем ![]() , если
, если ![]() , то есть в этом случае
, то есть в этом случае ![]() нулевая матрица.
нулевая матрица.
Сформулируем основную теорему данного раздела.
Теорема 5.Пусть ![]() точное решение системы
точное решение системы ![]() , в которой вектор
, в которой вектор ![]() и матрица
и матрица ![]() есть приближения вектора
есть приближения вектора ![]() и невырожденной (определитель
и невырожденной (определитель ![]() ) квадратной матрицы
) квадратной матрицы ![]() порядка m с известными относительными
погрешностями
порядка m с известными относительными
погрешностями ![]() и
и ![]() .
.
Если выполняется неравенство 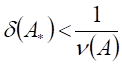 ,
, ![]() , или
, или ![]() , то для точного решения
, то для точного решения ![]() системы
системы ![]() справедлива следующая оценка
относительной погрешности приближения
справедлива следующая оценка
относительной погрешности приближения ![]() к
к ![]() :
:
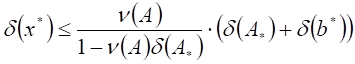 .
.
В случае отсутствия возмущения основной матрицы А
системы, тогда ![]() , имеем оценку из теоремы 1:
, имеем оценку из теоремы 1: ![]() .
.
Отметим, что когда ![]() (много меньше 1), можно использовать
более простую, но менее точную формулу:
(много меньше 1), можно использовать
более простую, но менее точную формулу:
![]() .
.
4. Пример исследования обусловленности вычислительной задачи с возмущенной системой ограничений ЗЛП
Во введении к статье был рассмотрен пример плохо обусловленной задачи линейного программирования, когда небольшое возмущение одного из коэффициентов уравнения системы ограничений приводит к совершенно другому решению. Сейчас мы рассмотрим аналог такой системы ограничений для удобства с меньшими коэффициентами и объясним причины такого явления, используя установленные теоремы,
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
Очевидно, задача имеет решение ![]() ,
, ![]() Находим число обусловленности
невырожденной матрицы
Находим число обусловленности
невырожденной матрицы 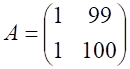 в норме при
в норме при ![]() , вычислив одним из известных
способов обратную матрицу
, вычислив одним из известных
способов обратную матрицу 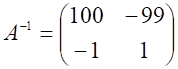 ,
,
![]()
Рассмотрим возмущенную систему ограничений
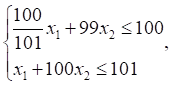 или
или 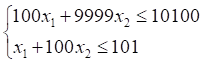 .
.
В первом неравенстве коэффициент 1 при
неизвестном ![]() заменен на
заменен на ![]() . Для этой задачи решением является
вектор
. Для этой задачи решением является
вектор ![]() ,
, ![]() . Разница между решениями по норме (p=1)
. Разница между решениями по норме (p=1) ![]() огромна.
огромна.
Матрица возмущенной системы 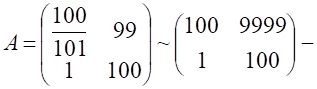 невырожденная, имеет обратную, но
если мы заменим коэффициент
невырожденная, имеет обратную, но
если мы заменим коэффициент ![]() приближенным значением
приближенным значением ![]() , то возмущенная система
, то возмущенная система 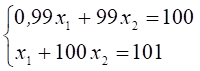 уже будет иметь вырожденную матрицу
уже будет иметь вырожденную матрицу 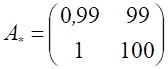 с матрицей возмущения
с матрицей возмущения 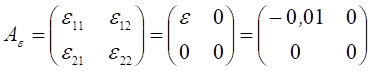 . Абсолютная погрешность приближения
составляет в применяемой нами норме величину
. Абсолютная погрешность приближения
составляет в применяемой нами норме величину ![]() . Устанавливаем, что достаточное
условие
. Устанавливаем, что достаточное
условие ![]() или
или 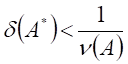 , не вырождения приближенной матрицы
, не вырождения приближенной матрицы ![]() не выполнено, так как верно обратное
неравенство
не выполнено, так как верно обратное
неравенство ![]() , которое равносильно неравенству:
, которое равносильно неравенству: 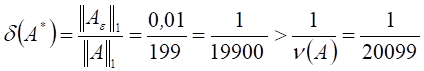 .
.
Достаточные условия теоремы 3 будут
выполнены, если задать ![]() ; тогда
; тогда ![]() и справедлива следующая оценка
относительной погрешности приближения решения
и справедлива следующая оценка
относительной погрешности приближения решения ![]() к решению
к решению ![]() (естественно, считаем
(естественно, считаем ![]() ):
): 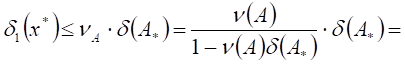
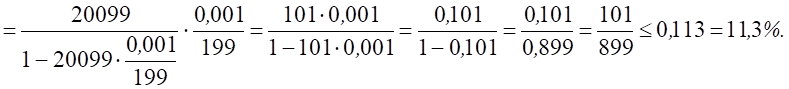 Относительная погрешность коэффициентов
матрицы
Относительная погрешность коэффициентов
матрицы ![]() имеет величину
имеет величину 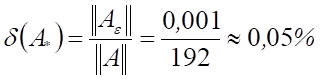 , это указывает на возможность
увеличения погрешности решения до 226 раз
, это указывает на возможность
увеличения погрешности решения до 226 раз ![]() .
.
Чтобы обеспечить вычисление приближенного
решения ЗЛП с заданной точностью, например, чтобы относительная погрешность ![]() решения составляла величину не больше
некоторого постоянного числа
решения составляла величину не больше
некоторого постоянного числа ![]() , достаточно требовать выполнения
неравенств:
, достаточно требовать выполнения
неравенств:
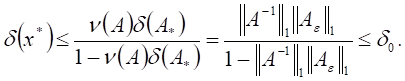
Отсюда имеем оценку абсолютной погрешности матрицы
приближения, или оценку матрицы
возмущения ![]() :
: 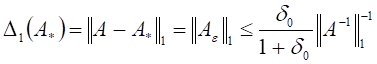 .
.
Если считать ![]() , то
, то 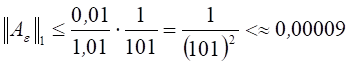 и коэффициент
и коэффициент ![]() в возмущенной системе ограничений можно
брать от 1 до 0,99991 включительно; остальные коэффициенты в системе считаем
точными или приближенными с примерно такого же порядка погрешностями (чтобы по
норме выполнялась оценка
в возмущенной системе ограничений можно
брать от 1 до 0,99991 включительно; остальные коэффициенты в системе считаем
точными или приближенными с примерно такого же порядка погрешностями (чтобы по
норме выполнялась оценка ![]() ). С такой точностью заданными
коэффициентами вычислительная задача хорошо обусловлена и может быть найдено
приближенное решение с требуемой точностью.
). С такой точностью заданными
коэффициентами вычислительная задача хорошо обусловлена и может быть найдено
приближенное решение с требуемой точностью.
Заключение
Подводя итоги исследования, следует отметить, что реализация разработанных авторами утверждений в виде ряда приведенных теорем позволяет потребителю эффективно проводить исследования процессов и объектов в экономике на основе линейных математических моделей и более обоснованно получать решения вычислительных задач при работе с приближенными данными. Значимую роль в увеличении погрешности решения вычислительной задачи ЗЛП играет структура матрицы системы ограничений, а не величина ее определителя.
Источники:
2. Данилина Н.И., Дубровская Н.С.,Кваша О.П.,Смирнов Г.Л. Вычислительная математика. - М: Высшая школа, 1985. – 475 c.
3. Воеводин В.В. Линейная алгебра. - М: Наука, 1980. – 400 c.
4. Амосов А.А., Дубинский Ю.А.,Копченова Н.В. Вычислительные методы для инженеров. / Учебное пособие. - М.: Высш. шк., 1994. – 543 c.
5. Като Т. Теория возмущений линейных операторов. - М.: Мир, 1972. – 740 c.
6. Акоф Р., Сасиени М. Основы исследования операций. - М.: Мир, 1971. – 534 c.
7. Попов А.М. Экономико-математические методы и модели. / Учебник для прикладного бакалавриата 2-е изд., испр. и доп. - М.: Юрайт, 2014. – 479 c.
8. Хуснутдинов Р.Ш. Экономико-математические методы и модели. / Учебное пособие. - М.: НИЦ ИНФРА-М, 2014. – 224 c.
9. Юдин С.В. Математика и экономико-математические модели. / Учебное пособие. - М.: ИЦ РИОР, 2016. – 374 c.
10. Волков И.К., Загоруйко Е.А. Исследование операций. / Учебник для вузов. - М.: Изд. МГТУ им Н. Э. Баумана, 2000. – 436 c.
11. Томас Х. Кормен и др. Глава 29. Линейное программирование. / Алгоритмы: построение и анализ — 2-е изд. - М.: «Вильямс», 2006.
12. Юдин Д.Б., Гольдштейн Е.Г. Задачи и методы линейного программирования. - М., 2010.
13. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1974. – 223 c.
14. Канторович Л.В., Акилов Г.П. Функциональный анализ. - М.: Наука, 1984. – 752 c.
15. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. / Изд. четвёртое, переработанное. - М.: Наука, 1976.
16. Марчук Г.И. Методы вычислительной математики. - Новосибирск: Наука, 1973. – 351 c.
17. Бабенко К.И. Основы численного анализа. - М.: Наука, 1986. – 743 c.
18. Бахвалов Н.С. Численные методы. / 3-е изд. - М., 2003.
19. Воеводин В.В. Математические основы параллельных вычислений. - М.: Изд-во МГУ, 1991. – 345 c.
20. Прасолов В.В. Задачи и теоремы линейной алгебры. - М.: Наука, Изд. фирма «Физ.-мат. лит.», 1996. – 302 c.
21. Стренг Г. Линейная алгебра и её применения. - М.:Мир, 1980. – 459 p.
22. Фаддеев Д.К. Лекции по алгебре. / 5-еизд. - СПб: Лань, 2007.
Страница обновлена: 26.12.2025 в 11:15:22
Download PDF | Downloads: 25
Evaluation of the solution to linear programming problems with approximate data in Lp-norms
Chuvenkov A.F., Rutta N.A., Stryukov M.B., Bolgova A.E.Journal paper
Informatization in the Digital Economy
Volume 4, Number 1 (January-March 2023)
Abstract:
The article considers the conditionality of solving correct computational linear programming problems (LPP) given in canonical form with inaccurately known matrix elements and a data vector.
The evaluation of the solution of linear programming problems is given in various Lp-norms.
Estimates of the error in solving linear programming problems with an approximately given right-hand side and with an approximately given matrix of coefficients are given in the form of theorems. In the form of theorems, estimates of the relative error of the inverse perturbation matrix and the absolute and relative errors of the approximate solution of linear programming problems in the general case with approximately specified coefficients of the constraints' system are obtained. The implementation of the authors' statements in the form of a number of the above theorems makes it possible to effectively conduct research on business processes in the digital economy based on linear mathematical models and more reasonably obtain solutions to computational problems when working with approximate data.
References:
Akof R., Sasieni M. (1971). Osnovy issledovaniya operatsiy [Operations research theory] M.: Mir. (in Russian).
Amosov A.A., Dubinskiy Yu.A.,Kopchenova N.V. (1994). Vychislitelnye metody dlya inzhenerov [Computational methods for engineers] M.: Vyssh. shk. (in Russian).
Babenko K.I. (1986). Osnovy chislennogo analiza [Numerical analysis] M.: Nauka. (in Russian).
Bakhvalov N.S. (2003). Chislennye metody [Numerical methods] M.. (in Russian).
Danilina N.I., Dubrovskaya N.S.,Kvasha O.P.,Smirnov G.L. (1985). Vychislitelnaya matematika [Computational Mathematics] M.: Vysshaya shkola. (in Russian).
Demidovich B.P., Maron I.A. (1970). Osnovy vychislitelnoy matematiki [Fundamentals of Computational Mathematics] M.: Nauka. (in Russian).
Faddeev D.K. (2007). Lektsii po algebre [Algebra lectures] SPb.: Lan. (in Russian).
Kantorovich L.V., Akilov G.P. (1984). Funktsionalnyy analiz [Functional analysis] M.: Nauka. (in Russian).
Kato T. (1972). Teoriya vozmushcheniy lineynyh operatorov [Perturbation theory of linear operators] M.: Mir. (in Russian).
Khusnutdinov R.Sh. (2014). Ekonomiko-matematicheskie metody i modeli [Economic and mathematical methods and models] M.: NITs INFRA-M. (in Russian).
Kolmogorov A.N., Fomin S.V. (1976). Elementy teorii funktsiy i funktsionalnogo analiza [Elements of function theory and functional analysis] M.: Nauka. (in Russian).
Marchuk G.I. (1973). Metody vychislitelnoy matematiki [Methods of computational mathematics] Novosibirsk: Nauka. (in Russian).
Popov A.M. (2014). Ekonomiko-matematicheskie metody i modeli [Economic and mathematical methods and models] M.: Yurayt. (in Russian).
Prasolov V.V. (1996). Zadachi i teoremy lineynoy algebry [Linear algebra problems and theorems] M.: Nauka, Izd. firma «Fiz.-mat. lit.». (in Russian).
Streng G. (1980). Lineynaya algebra i eyo primeneniya M.: Mir.
Tikhonov A.N., Arsenin V.Ya. (1974). Metody resheniya nekorrektnyh zadach [Methods for solving fuzzy problems] M.: Nauka. (in Russian).
Tomas Kh. Kormen i dr. (2006). Glava 29. Lineynoe programmirovanie [Chapter 29. Linear programming] M.: «Vilyams». (in Russian).
Voevodin V.V. (1980). Lineynaya algebra [Linear algebra] M.: Nauka. (in Russian).
Voevodin V.V. (1991). Matematicheskie osnovy parallelnyh vychisleniy [Mathematical basis of parallel computing] M.: Izd-vo MGU. (in Russian).
Volkov I.K., Zagoruyko E.A. (2000). Issledovanie operatsiy [Operations research theory] M.: Izd. MGTU im N. E. Baumana. (in Russian).
Yudin D.B., Goldshteyn E.G. (2010). Zadachi i metody lineynogo programmirovaniya [Linear programming problems and methods] M.. (in Russian).
Yudin S.V. (2016). Matematika i ekonomiko-matematicheskie modeli [Mathematics and economic and mathematical models] M.: ITs RIOR. (in Russian).
