Systemic risks in financial markets

1. Introduction

The cause and effect analysis of the 2007-2009 financial crisis has highlighted the problem of financial system risks. At a fundamental level, the notion of system risks surfaces in the analysis of mode change in the complex adaptive systems to which financial markets undoubtedly belong. Intuitively, a system risk is concerned with the effects of the interaction between economic actors that lead to substantial consequences for the whole system. It is, perhaps, impossible to give a laconic and precise definition of a system risk. The most complete descriptions are usually no more than detailed descriptions of possible scenarios that can be classified as “system risk-related”, for instance: see [1]. Quantitative analysis of system risks commands the attention of the Bank of Russia [2, 3], international organisations (International Monetary Fund) [4, 5, 6, 7] and academic science [9, 10, 11].

2. An inter-bank network as a directed, weighted graph

The starting point of any quantitative analysis of system risks in the inter-bank market will be the representation of the latter as a directed, weighted graph. Banks are located at the junctions of this graph, and their obligations to one another at the edges. Edge directions are conditional, but conventionally an edge is directed from the debtor to the creditor. Thus, in the matrix ‘W’ which characterises the graph under study

the edge with direction i ‑> j corresponds to the loan provided by the bank j to the bank i. Here the junctions having outbound edges correspond only to net borrowers, and the junctions having only inbound edges to net creditors. Finally, junctions with both inbound and outbound edges correspond to those banks that are creditors and borrowers at the same time. In all cases the values of the matrix elements are equal to the amounts of the corresponding loans. The above-described classification of junctions corresponds to a so-called ‘bow-tie’ decomposition of a directed graph into three main components; Out -> In-Out -> In. Fig.1 shows a bow-tie structure for the Russian Federation’s interbank-lending market:

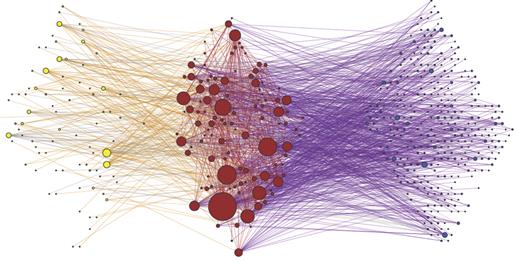
Figure 1. A component structure of the Russian Federation’s interbank-lending market [14]

The quantitative analysis of the component structure of the Russian Federation’s interbank-lending market that we have performed [12] has demonstrated that most banks (about 60 %) can be considered net borrowers. At the same time, as can be seen from Fig. 1, the majority of large banks reside within the In-Out sphere.

3. Multi-staged default: Gai-Kapadia’s model [12]

The creation of modern quantitative models of a multi-staged default in the interbank-lending market is largely based on pioneer work [12]. The mechanism of multi-staged spreading discussed in [12] is presented below. Let us consider a network junction (a bank) with an index i which has k-value of inbound edges and j-value of outbound edges, i.e. k = the borrowing bank, and о = crediting banks, each edge being “burdened” by the amount of the respective loan. Consider as an example the case where one of the borrowers k of the bank i becomes bankrupt. Propagation of the default takes place if the initial default results in the default of the bank i, i.е. when an institutionally established balance sheet gets disrupted for junction i as a result of the debtor-bank’s failure to discharge the debt. The balances of banks take into account assets A, including those related to the interbank-lending market (A^IB assets), and liabilities L. Thus, sufficiency of capital K_i for junction i is equal to K_i=A_i-L_i. Model [12] using the simplest supposition that A^IB assets, related to the interbank-lending, are equally distributed along the edges within the junction. According to these suppositions, the default of one market actor entails a default of the considered junction where

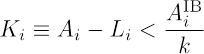
The main step in devising a multi-staged default mathematical model is the transition to a probabilistic description based on introducing the probability v_k of the junction default of the degree k at the default of one of the connections within this junction

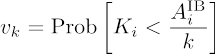
and also on the description of the interbank-lending market as a directed tree-graph with the distribution of probabilities along a number of inbound and outbound edges p_ik. Thus stated, the task reduces itself to a standard task of the percolation of the edges on a directed graph. When analysing risks on the interbank-lending market, work [12] mainly focuses on the issue of the probability of the appearance of a gigantic percolation cluster and the related market breakdown.

4. System risks in the Russian Federation’s interbank market [13, 14]

It would be interesting to summarise the results of work [12] and to develop a multi-staged default model taking into account the realistic topology of a weighted graph of the interbank-lending market, as well as realistic balance sheets of the banks. Such a model has been created for Russian interbank-lending market in works [13, 14].

The data given is sufficient to study the risks related to possible multi-staged defaults using numerical simulations. However, the possibility of analytical description depends on the complexity of a typical topology of default clusters. Numerical studies [13, 14] have revealed the following typical characteristics of multi-staged defaults:

· Conditional possibilities of the default propagation depend on the functional role (statements concerning the bow-tie structure of the interbank-lending graph) of the trigger junction and the junction receiving the default shock.

· Although the initial graph topology is quite different from the tree one and is, in particular, characterised by a high-degree of clusterisation, the default clusters are, in most cases, tree clusters.

· The multi-staged process under study is characterised by considerable dependence on the probabilistic interrelationship between the degrees of the neighboring junctions. For all of the studied networks this dependence corresponds to the presence of an expressed disassortativity, where a junction with large number of edges lies adjacent to a junction with small number of edges and vice versa.

An effective arboricity of the default clusters enables one to create a multi-staged default propagation model using a well-developed formalism of the generating functions, taking into account both the disassortativity of the interbank-lending network and the dependence of probability of the default propagation from the donor-junction to the recipient-junction [13,14]. Fig. 2. shows the comparison of the model forecasts with the results of numerical simulation for distribution according to the sizes of the default clusters.

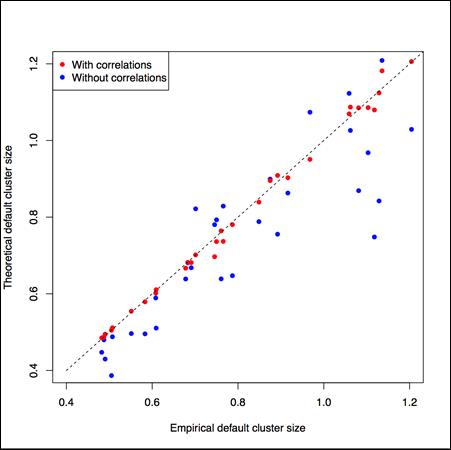
Figure 2. Empirical distribution according to the sizes of default clusters (dotted line) compared to the theoretical forecasts exclusive (blue) and inclusive (red)

of the correlations between the degrees of the adjacent junctions (disassortativity)

of the interbank-lending network. [14]

As can be seen from Fig. 2, taking into account disassortativity is extremely important for a realistic description of the multi-staged default process.

It has been mentioned above that the main type of system risks in the interbank-lending market studied in the pioneer work [12] and a number of subsequent works is the risk of the appearance of a gigantic default component, i.e. in the percolation mode. At the same time, the formalism methodology applied in works [12, 13, 14] enables us to evaluate whether the real interbank-lending network is in the percolation mode or not. A detailed analysis [14] has demonstrated that the Russian interbank-lending network has always been quite distant from the percolation point and, in this sense, it is resistant to the system risk discussed in work [12].

5. Conclusion

Finally, let us list our conclusions:

· Considering multi-staged defaults in the interbank-lending market is an important component of the analysis of system risks in financial markets.

· The analysis of data on the Russian Federation’s interbank-lending market shows that the respective system risks can be classified as those related to the non-percolative phase.

· The bow-tie structure of the respective directed graph and its disassortativity should be taken into account when creating an adequate mathematical model of system risks related to multi-staged defaults.

· Although the initial graph is characterised by considerable deviations from the tree topology, the graphs of multi-staged defaults are arborous.