Оптимизации затрат на жизненном цикле образца техники радиоэлектронной борьбы: применение методов регрессионного анализа и математического программирования
Аносов Р.С.1, Бывших Д.М.1, Зеленская С.Г.1, Пасичник В.А.1
1 НИИИ (РЭБ) ВУНЦ ВВС «ВВА» Научно-исследовательский испытательный институт (радиоэлектронной борьбы) военного учебно-научного центра Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», ,
Скачать PDF | Загрузок: 55 | Цитирований: 3
Статья в журнале
Экономика высокотехнологичных производств (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Том 1, Номер 1 (Январь-Март 2020)
Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=44198185
Цитирований: 3 по состоянию на 15.09.2025
Аннотация:
Рассмотрена модель управления входными характеристиками (параметрами качества) образца техники радиоэлектронной борьбы на начальных стадиях жизненного цикла для оптимизации стоимости последующих стадий и всего жизненного цикла. Сформулирована задача оптимизации затрат на полный жизненный цикл образца техники радиоэлектронной борьбы, которая формализована в виде задачи математического программирования по нахождению значений характеристик образца, обеспечивающих минимизацию затрат на полный жизненный цикл. При применении специальных корректирующих функций зависимости затрат на стадиях жизненного цикла от характеристик принимают линейный вид и оптимизационная задача сводится к задаче линейного программирования. Приведен пример решения этой задачи, в котором анализируются зависимости затрат от серийности и длительности эксплуатации при различных уровнях ограничений по выделяемым на начальные стадии ресурсам – затрат на научно-исследовательские и опытно-конструкторские работы в аспекте минимизации затрат на полный жизненный цикл образца.
Ключевые слова: полный жизненный цикл, стадия, оптимизация затрат, показатели качества
Введение. Концепция управления затратами жизненного цикла (Life-Cycle Costing, LCC [1] (Okano, 2001)) стала важнейшей технологией управления, которая должна коренным образом изменить порядок финансирования государственных проектов в оборонной отрасли. При этом стоимость полного жизненного цикла (ЖЦ) образца (от исследований возможностей и путей создания до его утилизации) становится наиболее важным показателем. В этом аспекте отмечается исключительная важность начальных стадий ЖЦ. «Все эксплуатационные свойства изделия – ремонтопригодность, надежность, экономичность – уже заложены на этапе проектирования и производства. Для сложных наукоемких изделий машиностроения, например, около 25% затрат на жизненный цикл приходятся на стадию проектирования и производства, а остальные 75 – на стадию эксплуатации и капитального ремонта [2]. Схожие оценки приводятся и для военной техники [3] (Polovinkin, Fomichev, 2016): 30% стоимости жизненного цикла военной техники приходится на этап разработок и производства, а 70% – на этап эксплуатации. Отметим, что доля затрат на эксплуатацию образцов техники радиоэлектронной борьбы (РЭБ) может достигать 80%. По оценкам специалистов, более половины имеющихся дефектов готовой машиностроительной продукции вызваны ошибками в конструкторских решениях, третья часть – недостатками технологии изготовления, и только 5–15% возникают по вине эксплуатирующей стороны» [2].
Модель затрат на ЖЦ. Таким образом, вкладывая некоторый ресурс в научно-исследовательские работы и опытно-конструкторские работы (НИРОКР), обеспечивается некоторый уровень качества (характеристик) образца, который в дальнейшем определяет как его эффективность по назначению, так и затраты на стадиях его жизненного цикла (ЖЦ): серийного производства (СП), эксплуатации (ЭКС) и капитального ремонта (КР). Можно ожидать, что определенному уровню характеристик образца будут соответствовать определенные уровни стоимости стадий жизненного цикла:
![]() , (1)
, (1)
где ![]() –
стоимость i-й стадии ЖЦ;
–
стоимость i-й стадии ЖЦ; ![]() - характеристики образца,
наиболее влияющие на стоимости стадий ЖЦ;
- характеристики образца,
наиболее влияющие на стоимости стадий ЖЦ; ![]() –
некоторая функция, определяющая стоимость i-й
стадии ЖЦ в зависимости от значений характеристик образца.
–
некоторая функция, определяющая стоимость i-й
стадии ЖЦ в зависимости от значений характеристик образца.
С учетом (1) общие затраты на весь ЖЦ составят:
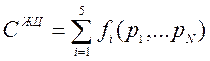 .
(2)
.
(2)
Задача оптимизации затрат на полном ЖЦ. С учетом (2) необходимо найти такие значения характеристик образца, при которых затраты на весь ЖЦ минимальны. Задачу формализуем в виде:
Найти
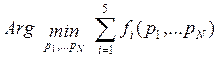 (3)
(3)
при
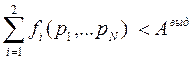 (4)
(4)
![]() , (5)
, (5)
где: ![]() –
ассигнования, выделяемые НИОКР;
–
ассигнования, выделяемые НИОКР; ![]() и
и
![]() –достигаемый уровень эффективности
образца и требуемый уровень соответственно.
–достигаемый уровень эффективности
образца и требуемый уровень соответственно.
Ограничение (4) отражает реальное положение по ограничению ассигнований на НИОКР. Ограничение (5) – требование по уровню эффективности образца.
Анализ затрат на НИОКР [4–6] (Anosov, Strokova, Garashchuk, 2013; Anosov, Strokova, Garashchuk, 2016; Akinshin, Starozhuk, 2013), серийное производство [7, 8] (Anosov, Byvshikh, Zelenskaya, 2018; Orlov, Strokova, Garashchuk, 2016), эксплуатацию [9–11] (Byvshikh, Zelenskaya, Strokova, 2017; Anosov, Boev, Byvshikh, Garashchuk, Pasichnik, Strokova, 2018; Anosov, Byvshikh, Orlov, 2017), капитальный ремонт [10, 11] (Anosov, Boev, Byvshikh, Garashchuk, Pasichnik, Strokova, 2018; Anosov, Byvshikh, Orlov, 2017), показывает, что зависимости стоимости этих стадий ЖЦ от характеристик образца могут иметь различный вид. Однако используя корректирующие функции [7] (Anosov, Byvshikh, Zelenskaya, 2018), можно перейти к линейной зависимости и построить линейную регрессию стоимости стадий как функции характеристик образца.
Таким образом, задача (3) – (5) сводится к задаче линейного программирования, которая решается известными методами [12] (Bandi, 1989).
Пример решения задачи. Рассмотрим далее для иллюстрации представленных положений следующий гипотетический пример. Пусть имеется некоторая статистика по N образцам техники РЭБ, включающая затраты на стадиях жизненного цикла и значения характеристик (табл. 1).
Таблица 1
Исходные данные по образцам (пример)
|
№ образца
|
|
|
|
|
|
Эффективность**, p1
|
Автоматизация*, p2
|
Ремонтопригодность*,
p3
|
Безотказность*, p4
|
Сохраняемость*,
p5
|
Контролепригодность*, p6
|
Модернизационная пригодность*, p7
|
|
1
|
0,65
|
0,6
|
0,575
|
0,375
|
0,425
|
0,625
|
0,475
|
0,55
|
0,6
|
0,6
|
0,6
|
0,635
|
|
2
|
0,6
|
0,625
|
0,575
|
0,425
|
0,0
|
0,6
|
0,35
|
0,6
|
0,6
|
0,06
|
0,05
|
0,575
|
|
3
|
0,75
|
0,75
|
0,65
|
0,4
|
0,425
|
0,775
|
0,75
|
0,55
|
0,75
|
0,725
|
0,75
|
0,725
|
|
4
|
0,85
|
0,9
|
0,8
|
0,0
|
0,325
|
0,75
|
0,5
|
0,75
|
0,9
|
0,85
|
0,875
|
0,875
|
|
5
|
1,0
|
0,825
|
0,75
|
0,4
|
0,425
|
0,725
|
0,95
|
0,55
|
0,775
|
0,775
|
0,5
|
0,8
|
|
6
|
0,1
|
0,0
|
0,25
|
0,2
|
0,15
|
0,0
|
0,0
|
0,1
|
0,15
|
0,2
|
0,2
|
0,0
|
|
7
|
0,0
|
0,12
|
0,0
|
0,1
|
0,05
|
0,05
|
0,0
|
0,0
|
0,0
|
0,1
|
0,1
|
0,1
|
|
8
|
0,9
|
1,0
|
0,85
|
0,9
|
1,0
|
1,0
|
0,89
|
0,9
|
0,95
|
1,0
|
1,0
|
1,0
|
|
9
|
0,85
|
0,9
|
1,0
|
1,0
|
0,95
|
0,9
|
1,0
|
1,0
|
0,825
|
0,95
|
0,925
|
0,85
|
|
10
|
1,0
|
0,85
|
0,925
|
0,85
|
0,925
|
0,95
|
0,825
|
0,95
|
1,0
|
0,725
|
0,875
|
0,9
|
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
|
N-1
|
0,35
|
0,4
|
0,4
|
0,625
|
0,65
|
0,3
|
0,3
|
0,45
|
0,4
|
0,5
|
0,375
|
0,3
|
|
N
|
0,775
|
0,725
|
0,65
|
0,2
|
0,1
|
0,75
|
0,7
|
1
|
0,675
|
0,625
|
0,825
|
0,675
|
|
*) нормированные
переменные
**) комплексный показатель, агрегирующий тактико-технические характеристики образца | ||||||||||||
Источник: составлено авторами.
Данные в таблице 1 нормированы по формуле [13]:
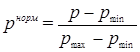 , (6)
, (6)
где
![]() – нормированное значение характеристики
(стоимости);
– нормированное значение характеристики
(стоимости); ![]() – реальное значение характеристики
(стоимости);
– реальное значение характеристики
(стоимости); ![]() – максимальное и минимальное
значения характеристики (стоимости). Для ряда характеристик использовались
экспертные оценки.
– максимальное и минимальное
значения характеристики (стоимости). Для ряда характеристик использовались
экспертные оценки.
Данные по характеристикам (табл. 1) скорректированы по соответствующим функциям [7] (Anosov, Byvshikh, Zelenskaya, 2018), применяя метод наименьших квадратов (МНК) [13] (Ayvazyan, Bushtaber, Enyukov, Meshalkin, 1989), можем построить множественные линейные регрессии для стоимости каждой стадии ЖЦ:
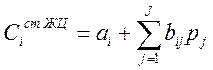 . (7)
. (7)
При применении МНК последовательно
для каждой стадии строится система нормальных уравнений, и определяются
значения коэффициентов ![]() :
:
![]() , (8)
, (8)
где: ![]() –
вектор-столбец коэффициентов регрессии;
–
вектор-столбец коэффициентов регрессии;
![]() – матрица реализаций
характеристик р;
– матрица реализаций
характеристик р;
![]() – вектор-столбец
реализаций стоимости.
– вектор-столбец
реализаций стоимости.
В результате получаем регрессии для всех стадий ЖЦ:
![]()
![]()
![]()
![]() (9)
(9)
![]()
Проводим для стоимостей стадий ЖЦ обратное для (6) преобразование. Общие затраты на все изделия на стадиях СП, КР, ЭКС зависят от объема серии (n) и длительности эксплуатации (T):
![]()
![]() (10)
(10)
![]()
![]()
![]()
Стоимость полного жизненного цикла как функция характеристик выразится как:
CЖЦ=0,0063+0,2510n+0,100nT+(0,4378 +0,0830n-0,0079nT)p1+
+(0,1657 +0,0618n-0,0135nT)p2+(0,2199 +0,0578n-0,0105nT)p3+ (11)
+(1,5061 + 0,2398n-0,0171nT)p4+(0,4813 +0,1763n-0,0136nT)p5+
+(0,3145 +0,0033n-0,0176nT)p6 +(0,5172 +0,2698n-0,010nT)p7
Результаты решения задачи (3) – (5) при различных значениях Авыд приведены в таблице 2. Положено, что ограничение (5) для рассматриваемых примеров выполняется.
Таблица 2
Результаты решения оптимизационной задачи (3) – (5) при различной серийности и длительности эксплуатации образца (в у.е.)
|
Авыд
|
|
|
|
|
|
CЖЦ мин
|
|
n=5, Т=20
| ||||||
|
0,5
|
0,027
|
0,459
|
0,745
|
6,89
|
0,835
|
8,9565
|
|
0,55
|
0,033
|
0,512
|
0,97
|
6,61
|
0,687
|
8,8121
|
|
0,6
|
0,038
|
0,551
|
1,139
|
6,4
|
0,575
|
8,7039
|
|
0,65
|
0,044
|
0,604
|
1,365
|
6,12
|
0,427
|
8,5595
|
|
0,7
|
0,048
|
0,644
|
1,534
|
5,91
|
0,316
|
8,4512
|
|
0,75
|
0,049
|
0,657
|
1,59
|
5,84
|
0,279
|
8,4152
|
|
1,0
|
0,049
|
0,657
|
1,59
|
5,84
|
0,279
|
8,415
|
|
n=10, Т=20
| ||||||
|
0,5
|
0,027
|
0,459
|
1,49
|
13,78
|
1,67
|
17,427
|
|
0,75
|
0,05
|
0,689
|
3,322
|
11,5
|
0,533
|
16,092
|
|
1,0
|
0,052
|
0,943
|
4,458
|
10,05
|
0,337
|
15,838
|
|
1,25
|
0,058
|
1,188
|
5,383
|
8,749
|
0,227
|
15,606
|
|
1,5
|
0,076
|
1,404
|
5,677
|
7,907
|
0,377
|
15,44
|
|
1,75
|
0,086
|
1,539
|
5,86
|
7,38
|
0,47
|
15,336
|
|
2,0
|
0,086
|
1,539
|
5,86
|
7,38
|
0,47
|
15,336
|
|
n=15, Т=20
| ||||||
|
0,5
|
0,0275
|
0,459
|
2,235
|
20,67
|
2,505
|
25,897
|
|
0,75
|
0,05
|
0,697
|
5,036
|
17,18
|
0,79
|
23,753
|
|
1,0
|
0,052
|
0,935
|
6,634
|
15,14
|
0,515
|
23,276
|
|
1,25
|
0,056
|
1,168
|
8,034
|
13,24
|
0,32
|
22,82
|
|
1,5
|
0,076
|
1,404
|
8,515
|
11,86
|
0,565
|
22,42
|
|
1,75
|
0,089
|
1,637
|
9,028
|
10,73
|
0,707
|
22,189
|
|
2,0
|
0,092
|
1,785
|
9,385
|
10,215
|
0,709
|
22,186
|
|
2,25
|
0,097
|
2,031
|
9,98
|
9,36
|
0,714
|
22,181
|
|
2,5
|
0,103
|
2,326
|
10,69
|
8,334
|
0,719
|
22,176
|
|
2,75
|
0,107
|
2,523
|
11,17
|
7,65
|
0,723
|
22,172
|
|
3,0
|
0,112
|
2,769
|
11,77
|
6,795
|
0,727
|
22,167
|
|
3,25
|
0,117
|
3,015
|
12,36
|
5,94
|
0,731
|
22,163
|
|
3,5
|
0,117
|
3,015
|
12,36
|
5,94
|
0,73125
|
22,163
|
|
n=15, Т=25
| ||||||
|
0,75
|
0,027
|
0,459
|
2,235
|
25,837
|
2,505
|
31,064
|
|
1,0
|
0,049
|
0,657
|
4,770
|
21,900
|
0,836
|
28,213
|
|
1,25
|
0,052
|
0,935
|
6,634
|
18,925
|
0,515
|
27,061
|
|
1,5
|
0,056
|
1,168
|
8,034
|
16,553
|
0,320
|
26,131
|
|
1,75
|
0,074
|
1,387
|
8,481
|
14,948
|
0,548
|
25,438
|
|
2,0
|
0,076
|
1,412
|
8,532
|
14,763
|
0,574
|
25,358
|
|
2,25
|
0,090
|
1,857
|
9,579
|
12,605
|
0,659
|
24,790
|
|
2,5
|
0,098
|
2,092
|
10,129
|
11,433
|
0,715
|
24,467
|
|
2,75
|
0,101
|
2,384
|
10,849
|
10,286
|
0,679
|
24,300
|
|
3,0
|
0,108
|
2,572
|
11,289
|
9,349
|
0,723
|
24,041
|
|
3,25
|
0,114
|
2,867
|
12,003
|
8,066
|
0,729
|
23,779
|
|
3,5
|
0,117
|
3,015
|
12,360
|
7,425
|
0,731
|
23,648
|
|
n=15, Т=30
| ||||||
|
0,75
|
0,027
|
0,459
|
2,235
|
31,005
|
2,505
|
36,231
|
|
1,0
|
0,049
|
0,657
|
4,770
|
26,280
|
0,836
|
32,593
|
|
1,25
|
0,059
|
0,937
|
6,174
|
23,096
|
0,735
|
31,001
|
|
1,5
|
0,058
|
1,185
|
8,068
|
19,716
|
0,338
|
29,364
|
|
1,75
|
0,074
|
1,387
|
8,481
|
17,938
|
0,548
|
28,428
|
|
2,0
|
0,086
|
1,539
|
8,790
|
16,605
|
0,705
|
27,726
|
|
2,25
|
0,090
|
1,857
|
9,579
|
15,126
|
0,659
|
27,311
|
|
2,5
|
0,098
|
2,092
|
10,129
|
13,719
|
0,715
|
26,753
|
|
2,75
|
0,102
|
2,277
|
10,575
|
12,757
|
0,718
|
26,429
|
|
3,0
|
0,105
|
2,595
|
11,364
|
11,278
|
0,672
|
26,015
|
|
3,25
|
0,114
|
2,867
|
12,003
|
9,680
|
0,729
|
25,392
|
|
3,5
|
0,117
|
3,015
|
12,360
|
8,910
|
0,731
|
25,133
|
Источник: составлено авторами.
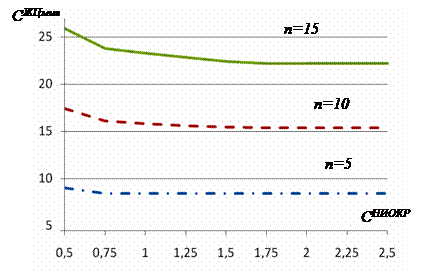 На основе данных таблицы
2 построены графики зависимости минимальных затрат на полный ЖЦ
от затрат на НИОКР (рис. 1 и 2).
На основе данных таблицы
2 построены графики зависимости минимальных затрат на полный ЖЦ
от затрат на НИОКР (рис. 1 и 2).
Рисунок 1. Зависимость минимизированных затрат на полный ЖЦ от затрат на НИОКР (СНИОКР) при длительности эксплуатации 20 лет и различных
объемах серии (пример)
Источник: составлено авторами.
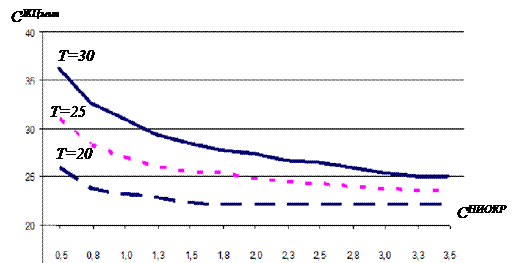
Рисунок 2. Зависимость минимизированных затрат на полный ЖЦ от затрат на НИОКР (СНИОКР) при объеме серии 15 изделий и различной длительности эксплуатации (пример)
Источник: составлено авторами.
Заключение. Отметим, что полученные результаты не претендуют на общность и полноту, носят частный характер и подразумевают необходимость уточнения, поскольку не рассматривались такие характеристики, как долговечность, уровень унификации, конструктивные особенности (транспортная база) и другие [14]. Представляется также целесообразным детализировать представленные модели затрат с выделением стоимостей этапов стадий ЖЦ (например, для ОКР – эскизный проект, технический проект, разработка конструкторской документации и т.д.). Требуют дальнейшего уточнения и доработки корректирующие функции [7] (Anosov, Byvshikh, Zelenskaya, 2018), описывающие влияние характеристик образца на стоимость стадий ЖЦ. Однако приведенный пример показывает значимость затрат на НИОКР в аспекте минимизации затрат на полный ЖЦ. В целом задача оптимизации затрат на полном жизненном цикле образца техники РЭБ может рассматриваться как задача комплексной оптимизации характеристик (показателей качества образца).
Пока в проблеме повышения качества техники РЭБ преобладает узкоаспектный подход – основное внимание уделяется обоснованию ограниченной номенклатуры основных тактико-технических требований (по назначению), непосредственно связанных с эффективностью образца. Значительно меньшее внимание уделяется обоснованию требований надежности и других характеристик качества, существенно влияющих на стоимость жизненного цикла образца. Однако такой подход ограничивает возможности повышения эффективности развития систем техники РЭБ, определяемой стоимостью перевода систем из исходного состояния в состояние с более высоким уровнем эффективности и поддержания систем в новом состоянии в течение заданного периода. Необходима методологическая общность, обеспечивающая возможность принятия комплексных управляющих решений на каждом этапе ЖЦ в интересах наиболее эффективного развития техники РЭБ и специальных систем [15] (Donskov, Anosov, Byvshikh, 2019), которую может дать предлагаемый подход к минимизации затрат на полном жизненном цикле при соответствующем развитии этого подхода.
Источники:
2. Антипов А. У качества нет «второй свежести» (Интервью с заместителем начальника Управления начальника вооружения ВС РФ по исследованиям генерал-лейтенантом А.А. Рахмановым). Красная звезда, 24 Марта 2005 года
3. Половинкин В.Н., Фомичев А.Б. Анализ причин нарушения сроков поставок в ОПК. Решение проблемы. Proatom.ru. [Электронный ресурс]. URL: http://www.proatom.ru/modules.php?name=News&file=article&sid=6782.
4. Аносов Р.С., Строкова Т.М., Гаращук Е.А. Методика оценки прогнозируемых затрат на НИР по разработке образцов радиоэлектронной техники военного назначения, не имеющих аналогов // Вооружение и экономика. – 2013. – № 1(22). – c. 61-70.
5. Аносов Р.С., Строкова Т.М., Гаращук Е.А. Методика оценки прогнозируемых затрат на ОКР по разработке образцов радиоэлектронной техники военного назначения, не имеющих аналогов // Вооружение и экономика. – 2016. – № 1(34). – c. 74-79.
6. Акиншин О.Н., Старожук Е.А. Методика определения базисной цены на НИОКР образцов вооружения // Известия Тульского государственного университета. Технические науки. – 2013. – № 1. – c. 348-356.
7. Аносов Р.С., Бывших Д.М., Зеленская С.Г. Прогнозирование стоимости средств измерений // Радиопромышленность. – 2018. – № 4. – c. 76-84.
8. Орлов В.А., Строкова Т.М., Гаращук Е.А. Методика оценки прогнозируемых затрат на серийное производство образцов радиоэлектронной техники военного назначения, не имеющих аналогов // Вооружение и экономика. – 2016. – № 3(36). – c. 29-34.
9. Бывших Д.М., Зеленская С.Г., Строкова Т.М. Оценка эффективности внедрения инноваций в образцах техники радиоэлектронной борьбы: использование автоматизированного информационно-расчетного комплекса // Энергия - XXI век. – 2017. – № 2(98). – c. 38-54.
10. Аносов Р.С., Боев А.С., Бывших Д.М., Гаращук Е.А., Пасичник В.А., Строкова Т.М. Прогнозирование технико-экономических показателей образцов техники радиоэлектронной борьбы. - Воронеж: Изд-во ВУНЦ ВВС «ВВА», 2018. – 226 c.
11. Аносов Р.С., Бывших Д.М., Орлов В.А. Методы оценки экономического эффекта различных стратегий технического обслуживания и ремонта техники РЭБ // Ремонт. Восстановление. Модернизация. – 2017. – № 5. – c. 25-29.
12. Банди Б. Основы линейного программирования. / пер. с англ. - М.: Радио и связь, 1989. – 176 c.
13. Айвазян С.А., Буштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Классификация и снижение размерности. / Справочное изд-е. - М.: Финансы и статистика, 1989. – 608 c.
14. ГОСТ 27.002-89. Надежность в технике. Основные понятия. Термины и определения
15. Донсков Ю.Е., Аносов Р.С., Бывших Д.М. Особенности управления развитием системы вооружения радиоэлектронной борьбы // Военная мысль. – 2019. – № 11. – c. 69-77.
16. Андерсон Т. Введение в многомерный статистический анализ. / пер. с англ. - М.: Физматгиз, 1963. – 500 c.
17. Кульбак С. Теория информации и статистика. / Пер. с англ. - М.: Наука, 1967. – 408 c.
Страница обновлена: 04.03.2026 в 12:24:05
Download PDF | Downloads: 55 | Citations: 3
Costs optimization on the life cycle of the electronic warfare equipment sample: application of regression analysis and mathematical programming methods
Anosov R.S., Byvshikh D.M., Zelenskaya S.G., Pasichnik V.A.Journal paper
High-tech Enterprises Economy
Volume 1, Number 1 (January-March 2020)
Abstract:
A model for controlling the input characteristics (quality parameters) of the electronic warfare equipment sample at the initial stages of the life cycle is considered to optimize the cost of subsequent stages and the entire life cycle. The optimization problem of the full lifecycle cost of electronic warfare design techniques, which is formalized as a mathematical programming problem of finding characteristic values of the sample, ensuring minimization of costs for the full life cycle, are formulated. When using special correction functions, the cost dependencies at the stages of the life cycle on the characteristics take a linear form; and the optimization problem is reduced to a linear programming problem. An example of solving this problem is given. THe authors analyzed the dependence of costs on seriality and duration of operation at different levels of restrictions on the resources allocated at the initial stages – the cost of R&D in the aspect of minimizing the cost of the sample full life cycle.
Keywords: full life cycle, stage, cost optimization, quality indicators
References:
Akinshin O.N., Starozhuk E.A. (2013). Metodika opredeleniya bazisnoy tseny na NIOKR obraztsov vooruzheniya [Methodology for determining the base price for R&D of weapons samples]. "Proceedings of the TSU" (Izvestija Tulskogo gosudarstvennogo universiteta). (1). 348-356. (in Russian).
Anderson T. (1963). Vvedenie v mnogomernyy statisticheskiy analiz [Introduction to multivariate statistical analysis] M.: Fizmatgiz. (in Russian).
Anosov R.S., Boev A.S., Byvshikh D.M., Garaschuk E.A., Pasichnik V.A., Strokova T.M. (2018). Prognozirovanie tekhniko-ekonomicheskikh pokazateley obraztsov tekhniki radioelektronnoy borby [Forecasting of technical and economic indicators of electronic warfare equipment samples] Voronezh: Izd-vo VUNTs VVS «VVA». (in Russian).
Anosov R.S., Byvshikh D.M., Orlov V.A. (2017). Metody otsenki ekonomicheskogo effekta razlichnyh strategiy tekhnicheskogo obsluzhivaniya i remonta tekhniki REB [Assessment methods for economic effect of different strategies of maintenance and repair of electronic warfare equipment]. Remont. Vosstanovlenie. Modernizatsiya. (5). 25-29. (in Russian).
Anosov R.S., Byvshikh D.M., Zelenskaya S.G. (2018). Prognozirovanie stoimosti sredstv izmereniy [Forecasting the cost of the means of measuring]. Radiopromyshlennost. (4). 76-84. (in Russian).
Anosov R.S., Strokova T.M., Garaschuk E.A. (2013). Metodika otsenki prognoziruemyh zatrat na NIR po razrabotke obraztsov radioelektronnoy tekhniki voennogo naznacheniya, ne imeyushchikh analogov [Technique of an estimation of predicted expenses for research works on working out of samples of the radio-electronic military-oriented technics which does not have analogues]. Vooruzhenie i ekonomika. (1(22)). 61-70. (in Russian).
Anosov R.S., Strokova T.M., Garaschuk E.A. (2016). Metodika otsenki prognoziruemyh zatrat na OKR po razrabotke obraztsov radioelektronnoy tekhniki voennogo naznacheniya, ne imeyushchikh analogov [Technique of an estimation of predicted expenses for developmental works on working out of samples of the radio-electronic military-oriented technics which does not have analogues]. Vooruzhenie i ekonomika. (1(34)). 74-79. (in Russian).
Ayvazyan S.A., Bushtaber V.M., Enyukov I.S., Meshalkin L.D. (1989). Prikladnaya statistika: Klassifikatsiya i snizhenie razmernosti [Applied statistics: classification and dimensionality reduction] M.: Finansy i statistika. (in Russian).
Bandi B. (1989). Osnovy lineynogo programmirovaniya [Basics of linear programming] M.: Radio i svyaz. (in Russian).
Byvshikh D.M., Zelenskaya S.G., Strokova T.M. (2017). Otsenka effektivnosti vnedreniya innovatsiy v obraztsakh tekhniki radioelektronnoy borby: ispolzovanie avtomatizirovannogo informatsionno-raschetnogo kompleksa [Evaluation of the efficiency of introduction of innovations in samples of technology of radioelectronic struggle: use of the automatic-informed information clearing complex]. Energiya - XXI vek. (2(98)). 38-54. (in Russian).
Donskov Yu.E., Anosov R.S., Byvshikh D.M. (2019). Osobennosti upravleniya razvitiem sistemy vooruzheniya radioelektronnoy borby [The distinctive features of managing weapon development for electronic warfare]. Voennaya mysl. (11). 69-77. (in Russian).
Kulbak S. (1967). Teoriya informatsii i statistika [Information theory and statistics] M.: Nauka. (in Russian).
Okano K. (2001). Life cycle costing – An approach to life cycle cost management: A consideration from historical development Asia Pacifìc Management Review. 6 (3). 317-341.
Orlov V.A., Strokova T.M., Garaschuk E.A. (2016). Metodika otsenki prognoziruemyh zatrat na seriynoe proizvodstvo obraztsov radioelektronnoy tekhniki voennogo naznacheniya, ne imeyushchikh analogov [A method of predictive cost estimation of military full-scale radio electronics samples production for lack of analogues]. Vooruzhenie i ekonomika. (3(36)). 29-34. (in Russian).
