Критерии оценки эффективности системы управления рисками
Скачать PDF | Загрузок: 33
Статья в журнале
Российское предпринимательство *
№ 6 (54), Июнь 2004
* Этот журнал не выпускается в Первом экономическом издательстве
Аннотация:
В предыдущем номере журнала [1] отмечалось, что в качестве статистических мер риска чаще всего используют: а) среднее квадратическое отклонение (волатильность) показателей деятельности организации или отдельных факторов риска за установленный период времени; б) значение волатильности, приходящееся на единицу ожидаемого дохода; в) вероятность возникновения заданных убытков за конкретный промежуток времени; г) максимальная величина потерь, которая не будет превышена с заданной вероятностью за фиксированный промежуток времени и другие показатели. Целесообразно рассмотреть эти методы оценки риска более детально.
Ключевые слова: риски, система управления рисками, методы оценки эффективности
Продолжение. Начало в №№ 11, 12/2003, 4, 5 /2004
В предыдущем номере журнала [1] отмечалось, что в качестве статистических мер риска чаще всего используют: а) среднее квадратическое отклонение (волатильность) показателей деятельности организации или отдельных факторов риска за установленный период времени; б) значение волатильности, приходящееся на единицу ожидаемого дохода; в) вероятность возникновения заданных убытков за конкретный промежуток времени; г) максимальная величина потерь, которая не будет превышена с заданной вероятностью за фиксированный промежуток времени и другие показатели. Целесообразно рассмотреть эти методы оценки риска более детально.
Статистические методы оценки рисков
Дисперсия (среднее квадратическое отклонение). В качестве меры риска дисперсия впервые использована в 1952 году. Автором предложения был американский экономист Гарри Марковиц, ставший впоследствии Нобелевским лауреатом. Это было первое количественное измерение риска. Как известно, дисперсия (или среднее квадратическое отклонение, вычисляемое как корень квадратный из дисперсии) является статистической величиной, определяющей степень изменчивости (волатильности) фактора риска (рис. 1).
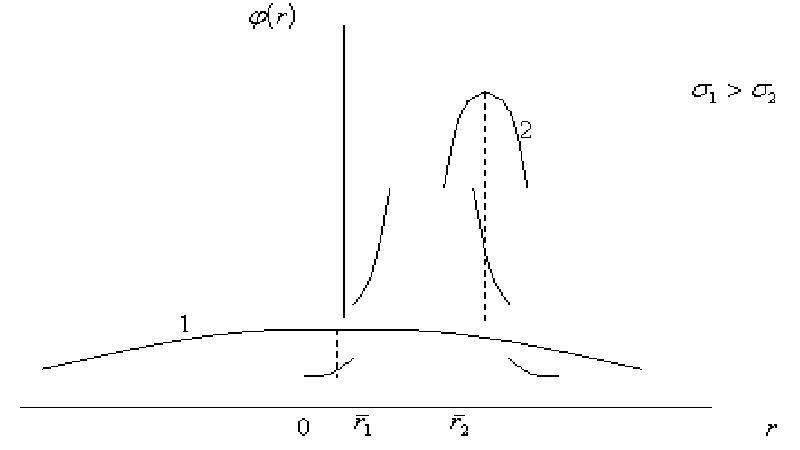
Рис. 1. Среднее квадратическое отклонение как мера риска
На рис. 1 представлены законы распределения доходностей (![]() ) двух финансовых инструментов. Причём, среднее квадратическое отклонение доходностей первого инструмента (
) двух финансовых инструментов. Причём, среднее квадратическое отклонение доходностей первого инструмента (![]() ) превышает среднее квадратическое отклонение доходностей второго инструмента (
) превышает среднее квадратическое отклонение доходностей второго инструмента (![]() ). Такая ситуация приводит к большей вероятности получения какого-то заданного убытка при инвестировании денежных средств в первый инструмент.
). Такая ситуация приводит к большей вероятности получения какого-то заданного убытка при инвестировании денежных средств в первый инструмент.
При вычислении дисперсии изменений рыночных цен можно использовать тот факт, что для небольших временных горизонтов значение этого показателя пропорционально длительности данного временного горизонта. Например, если известно значение дисперсии для временного горизонта в один день (![]() ), то значение дисперсии для временного горизонта в Т дней будет равно
), то значение дисперсии для временного горизонта в Т дней будет равно
![]() или
или ![]() .
.
Недостатком рассмотренной меры риска является сложность её использования, например, при сопоставлении рискованности вложения денежных средств в различные объекты инвестирования. Дело в том, что доходность и риск по инвестициям находятся в определенной зависимости. Как правило, инвестициям с большей доходностью соответствует больший риск. В этом случае для оценки риска целесообразно использовать относительные показатели, связывающие риск и доходность. Другим недостатком дисперсии как меры риска является то, что она в явном виде не указывает на возможные убытки.
Коэффициент вариации. Коэффициент вариации (![]() ) представляет собой отношение среднего квадратического отклонения к ожидаемому (среднему) значению (
) представляет собой отношение среднего квадратического отклонения к ожидаемому (среднему) значению (![]() ).
).
![]() .
.
Если в качестве среднего выступает ожидаемая доходность, то данный показатель характеризует величину риска, приходящуюся на единицу доходности. Чем выше коэффициент вариации, тем сильнее колеблемость и тем выше риск.
Коэффициент Шарпа. Коэффициент Шарпа (![]() ) представляет собой отношение средней доходности, превышающей безрисковую процентную ставку (
) представляет собой отношение средней доходности, превышающей безрисковую процентную ставку (![]() ), к среднему квадратическому отклонению доходности актива за весь период:
), к среднему квадратическому отклонению доходности актива за весь период:
![]() .
.
Использование безрисковой процентной ставки позволяет исключить из рассмотрения рисковые вложения с доходностью ниже, чем по государственным краткосрочным облигациям.
Коэффициент Трейнора. Коэффициент Трейнора (![]() ) представляет собой отношение средней доходности, превышающей безрисковую процентную ставку, к систематическому риску (
) представляет собой отношение средней доходности, превышающей безрисковую процентную ставку, к систематическому риску (![]() ):
):
![]() .
.
В отличие от коэффициента Шарпа в данном показателе доходность соотносится не с общим риском, а только с систематическим (недиверсифицируемым).
Недостатком рассмотренных показателей риска, как уже отмечалось, является то, что они прямо ничего не говорят о возможных потерях (убытках). Ведь именно это, прежде всего, интересует инвестора. Свободным от этого недостатка является показатель VaR.
Показатель VaR (Value at Risk). Показатель VaR (рисковая стоимость, или стоимость за риском) – это выраженная в денежных единицах оценка некоторой величины, которую не превысят ожидаемые в течение заданного периода времени и с заданной вероятностью потери портфеля финансовых инструментов (открытых позиций) под воздействием рыночных факторов риска [2,3].
На рис. 2 представлена плотность вероятностей доходностей некоторого портфеля финансовых инструментов. VaR этого портфеля для заданных доверительного интервала (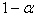 ) и периода удержания позиций t определяется как такое значение убытка (отрицательной доходности относительно ожидаемого значения), которое не будет превышено за время t с вероятностью (
) и периода удержания позиций t определяется как такое значение убытка (отрицательной доходности относительно ожидаемого значения), которое не будет превышено за время t с вероятностью (![]() ). То есть, для любого значения убытка x
). То есть, для любого значения убытка x
![]() ,
,
где ![]() вероятность того, что x не превысит VaR.
вероятность того, что x не превысит VaR.
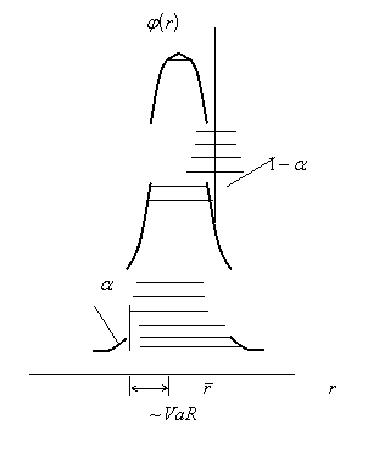
Рис. 2. Показатель VaR как мера риска
Как следует из данного определения, величина VaR для портфеля рассматриваемой структуры – это наибольший ожидаемый убыток, обусловленный колебаниями рыночных цен, который рассчитывается:
на определённый период времени в будущем (временной горизонт);
с заданной вероятностью его превышения (доверительный интервал);
при данном предположении о характере поведения рынка (рынок стабилен и ликвиден).
Например, фраза «Недельный 99-процентный VaR по облигациям составил миллион рублей» означает, что по открытым позициям в данном виде облигаций ожидаемые потери из-за рыночных рисков за неделю не превысят с вероятностью 99% одного миллиона рублей при условии сохранения рыночной конъюнктуры (см. рис. 2).
Метод оценки риска с помощью показателя VaR в общем случае предусматривает нормальный закон распределения логарифмических доходностей (натурального логарифма отношения цен ![]() к
к 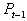 , зафиксированных в периоды измерения
, зафиксированных в периоды измерения ![]() и
и ![]() соответственно):
соответственно):
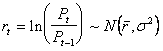 ,
,
где ![]() – логарифмическая доходность, распределенная по нормальному
– логарифмическая доходность, распределенная по нормальному
закону ![]() с математическим ожиданием
с математическим ожиданием ![]() и средним
и средним
квадратическим отклонением![]() .
.
Такая ситуация получается при непрерывном начислении процентов. В этом случае
![]() .
.
Предположение о нормальном законе распределения изменений факторов риска значительно облегчает вычисление показателя VaR. В этом случае распределение доходностей портфелей, состоящих из финансовых инструментов с линейными ценовыми характеристиками, будет также нормальным. Кроме того, в случае нормального распределения доверительный интервал (![]() ) характеризуется единственным параметром – квантилем (
) характеризуется единственным параметром – квантилем (![]() ). Квантиль показывает положение искомого значения случайной величины относительно среднего значения
). Квантиль показывает положение искомого значения случайной величины относительно среднего значения ![]() , выраженное в количестве стандартных отклонений
, выраженное в количестве стандартных отклонений ![]() .
.
Для расчёта показателя VaR необходимо рассмотреть инвестиционную позицию, например, состоящую из единицы какого-либо актива. Размер дневной прибыли (убытка) по такой позиции будет равен изменению цены актива за день. В этом случае наименьшая ожидаемая цена следующего дня с заданной вероятностью (![]() ) будет равна
) будет равна
![]() .
.
Математическое ожидание однодневного дохода обычно принимают равным нулю (![]() ). Волатильность доходности
). Волатильность доходности ![]() может быть оценена на основе исторических данных или на основе прогноза.
может быть оценена на основе исторических данных или на основе прогноза.
Значение VaR , отражающее наибольшее ожидаемое изменение цены за один день, определяется следующим образом:
![]() .
.
Используя разложение функции в ряд Тейлора, можно для малых величин ![]() записать
записать
![]() .
.
Отсюда выражение для VaR будет иметь следующий вид:
![]() .
.
В выражении для VaR знак минус опущен, так как обычно используют абсолютные значения этого показателя.
Для отдельной позиции, состоящей из нескольких инструментов, подверженных единственному фактору риска, величина VaR с временным горизонтом Т дней и доверительным интервалом (![]() ) может быть рассчитана по следующей формуле:
) может быть рассчитана по следующей формуле:
![]() ,
,
где V – текущая стоимость позиции (произведение текущей цены на количество единиц актива).
Центральной проблемой при расчете VaR является нахождение дисперсии доходности инструмента (для единичной позиции) или для портфеля в целом.
Следует отметить, что VaR – это оценка возможных потерь «сверху», она предусматривает очень большой и, следовательно, дорогой запас.
Метод оценки риска с помощью показателя VaR имеет существенные ограничения, основными причинами которых являются следующие:
1) далеко не всегда выполняется основополагающая посылка о нормальном законе распределения доходностей. Реальное распределение изменений цен обычно характеризуется значительным эксцессом, то есть, более «толстыми» хвостами и «острыми» вершинами по сравнению с нормальным законом распределения. Это приводит к тому, что показатель VaR недооценивает риск из-за экстремальных значений факторов. Выходом из этого положения может быть использование других моделей распределения случайных величин (распределения Стьюдента, Лапласа, Вейбулла и др.);
2) процессы на финансовых рынках в общем случае нестационарны. То есть, и математические ожидания доходности, и дисперсии изменяются во времени. Это приводит к тому, что использование исторических данных для расчета дисперсии может приводить к значительным погрешностям;
3) оценка риска с помощью показателя VaR эффективна только для портфелей (позиций), созданных из ликвидных активов. Если рынок активов или инструментов неликвиден, то просто не существует надежных цен для вычисления показателей доходности. В этом случае показатель VaR недооценивает размах возможных потерь;
4) низкая точность оценки риска с помощью показателя VaR для инструментов с нелинейными ценовыми характеристиками. Речь в первую очередь идет о портфелях, содержащих опционные контракты;
5) существует так называемый модельный риск. Если выбранная модель неточна, то действительные потери могут оказаться большими, чем предсказывает показатель VaR.
По указанным причинам метод оценки риска с помощью показателя VaR редко используется изолированно. Часто совместно с ним применяются различные методы сценарного анализа, которые будут рассмотрены в последующих номерах журнала.
Источники:
2. Энциклопедия финансового риск-менеджмента / Под ред. А. А. Лобанова и А. В. Чугунова. – М.: Альпина Паблишер, 2003. – 786 с.
3. Бартон Т., Шенкир У., Уокер П. Комплексный подход к риск- менеджменту: стоит ли этим заниматься / Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 208 с.
Страница обновлена: 18.02.2026 в 06:44:50
Download PDF | Downloads: 33
Kriterii otsenki effektivnosti sistemy upravleniya riskami
Selyukov V.K.Journal paper
