Моделирование взаимосвязи макроэкономических факторов и спроса на инновации

Введение

Изучение особенностей инновационного развития экономики России не теряет своей актуальности уже много лет. Несмотря на все усилия, общий уровень инновационной активности в России, то есть процент инновационных предприятий, ниже, чем зарубежных (рис. 1). Масштабы инновационной деятельности в России свидетельствуют о наличии резервов [5 с. 3725–3726; 7, с. 107] (Zagidullina, Zaynullina, Mavlyutova, Sirazetdinova, 2017, р. 3725–3726; Kleshcheva, 2012, р. 107).

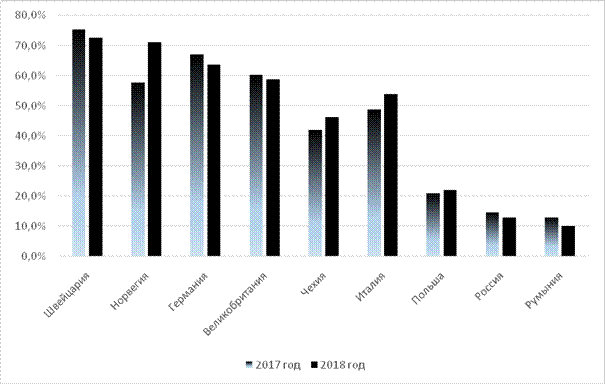
Рисунок 1. Совокупный уровень инновационной активности предприятий

Источник: Индикаторы инновационной деятельности: 2020: статистический сборник [6, с. 300–301] (Gokhberg, Ditkovskiy, Evnevich et al., 2020, р. 300–301).

Инновационные проекты требуют, как правило, больших капиталовложений [1, с. 49; 2, с. 125; 12, с. 89–90] (Azhimov, Fayzullin, Azhimova, 2018, р. 49; Bakhareva, 2017, р. 125; Sayfullina, 2010, р. 89–90). Поэтому необходимо совершенствование методов оценки их эффективности. Инновации – это коммерчески успешные новые идеи. Инвестиции в инновационный проект сопряжены с большим риском [19, с. 89] (Shagiakhmetova, Serdarova, 2018, р. 89), в первую очередь по причине сложности прогнозирования спроса на новый продукт, а следовательно, и коммерческого успеха. Повышение достоверности прогноза спроса позволит точнее оценивать эффективность инновационных проектов и снизить риск. В этом случае можно ожидать роста инновационной активности.

В научной литературе исследования, связанные с оценкой спроса, ведутся в различных направлениях. В работе Васильевой Е.Ю. исследуются особенности оценки влияния рисков на спрос в инновационной деятельности [4, с. 215–217] (Vasileva, 2020, р. 215–217). Симонов А.Б., Рогачев А.Ф., Симонова И.Э. [13, с. 45–46] (Simonov, Rogachev, Simonova, 2020, р. 45–46) на основе моделей спроса и предложения анализируют влияние эластичности спроса и предложения на результативность инновационной деятельности. Хорев А.В., Семенова С.В., Кропотова И.В., Оскирко А.В. [17, с. 129–132] (Khorev, Semenova, Kropotova, Oskirko, 2012, р. 129–132) исследуют возможность применения корреляционно-регрессионного анализа для прогнозирования влияния на спрос ценовых и неценовых, а также макроэкономических факторов. Тоткало Г.В. и Хрипунова А.С. [14, с. 77–78] (Totkalo, Khripunova, 2015, р. 77–78) провели анализ методов прогнозирования и программирования спроса. В работе Кузовкина А.И. [9, с. 29–30] (Kuzovkin, 2014, р. 29–30) изучается взаимосвязь спроса, цены на электроэнергию и темпа роста внутреннего валового продукта на основе построения регрессионной зависимости. Модель Басса в качестве основы для построения прогноза спроса на инновационный продукт предлагают применять Бурмистрова И.К., Кублин И.М., Сулян Г.C., Тинякова В.И. [3, с. 60] (Burmistrova, Kublin, Sulyan, Tinyakova, 2018, р. 60). Мазурова О.В. [10, с. 75–77] (Mazurova, 2018, р. 75–77) исследует, насколько меняется точность прогнозных оценок спроса для различных товаров в зависимости от горизонта прогнозирования. Поспелова Л.Я., Шананин А.А. [11, с. 26–27] (Pospelova, Shananin, 2019, р. 26–27) адаптируют нейронные сети для прогнозирования спроса в розничной торговле.

Целью данного исследования является построение экономико-математической модели, описывающей зависимость спроса на инновации от различных факторов. Научная новизна заключается в разработке модели оценки спроса на инновации на ранних стадиях проектирования на основе прогнозирования доходов потенциальных потребителей с использованием регрессии на главные компоненты. Гипотеза состоит в повышении достоверности прогнозирования на основе построенной модели.

Методика

Прогнозирование спроса является сложной и многоаспектной задачей, так как спрос подвержен влиянию множества внешних и внутренних факторов. На первых этапах разработки проекта часто бывает необходимо выбрать наиболее эффективные из нескольких альтернатив. В этом случае не всегда целесообразно организовывать опрос потенциальных покупателей. На начальных этапах разработки проекта возможна оценка спроса на основе анализа доходов населения. Прирост доходов необходимо рассматривать с учетом влияния инфляции [8, с. 948–949] (Kleshcheva, Sayfullina, 2019, р. 948–949).

В качестве метода построения модели зависимости прироста реальных доходов населения от факторов внешней макросреды была рассмотрена регрессия на главные компоненты [16, с. 246–249; 20, с. 82–88] (Pomerantsev, 2014, р. 246–249; Esbensen Kim, 2005, р. 82–88). В случае применения этого метода матрица факторов внешней среды вначале подвергается разложению с использованием метода главных компонент. Это позволяет уточнить только релевантную информацию. Затем строится регрессионная модель зависимости результирующего фактора от главных компонент. Применительно к рассматриваемой задаче вначале определяются главные компоненты, то есть основные направления изменений в экономике России, а затем рассчитывается зависимость от них прироста доходов населения.

Нахождение главных компонент предполагает построение модели [20, с. 152–153] (Esbensen Kim, 2005, р. 152–153):

X = T P^T + E, (1)

где Х – матрица исходных данных;

Т – матрица счетов;

Р – матрица нагрузок;

Е – матрица остатков.

Первоначально устанавливаются исходные значения = столбец матрицы X_a-1, обладающий максимальной остаточной суммой квадратов. Затем для первой главной компоненты рассчитывается:

(2)

(3)

(4)

(5)

Вклад первой главной компоненты вычитается:

(6)

Алгоритм повторятся для нахождения остальных главных компонент.

Регрессия у строится на векторы счетов . Для нахождения регрессионных коэффициентов используется формула:

(7)

где X-нагрузки являются нагрузками для рассматриваемых главных компонент, а Y-нагрузки определяются по формуле:

(8)

Результаты и обсуждения

Для расчета регрессионной модели нами были использованы данные по основным параметрам развития экономики России с 1999 по 2019 год (табл. 1).

Таблица 1

Параметры экономического развития России

В процессе расчетов на основе значений показателя остаточной дисперсии было определено, что для построения регрессионной модели необходимо использовать первую главную компоненту. Она описывают 83% вариации исходных данных.

Применение регрессии на главные компоненты предполагает расчет и анализ значений нагрузок и счетов по построенной модели. Нагрузки дают информацию о направлении главных компонент. Чем больше абсолютное значение нагрузок по фактору, тем больше этот фактор влияет на направление главной компоненты. Анализируя величины нагрузок (рис. 2), можно сделать вывод об экономической интерпретации главной компоненты.

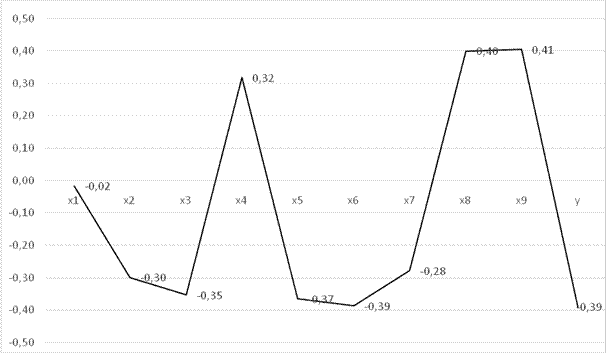Рисунок 2. Величина нагрузок по первой главной компоненте [1]

Источник: рассчитано автором на основе данных Федеральной службы государственной статистики.

Направление первой главной определяют следующие факторы: ставка рефинансирования (-0,35 [2]), индекс потребительских цен (-0,37), уровень безработицы (-0,39), инвестиции в основной капитал (0,40), динамика среднедушевых доходов населения (0,41), прирост реальных доходов населения (-0,39). Эта главная компонента интерпретируется как фактор цикличности развития экономической системы.

Счетами в модели регрессии на главные компоненты называются проекции исходных экономических периодов на главную компоненту. Анализ счетов дает возможность обобщить итоги экономического развития за представленный промежуток времени. На рисунке 3 представлены значения счетов для первой главной компоненты построенной модели.

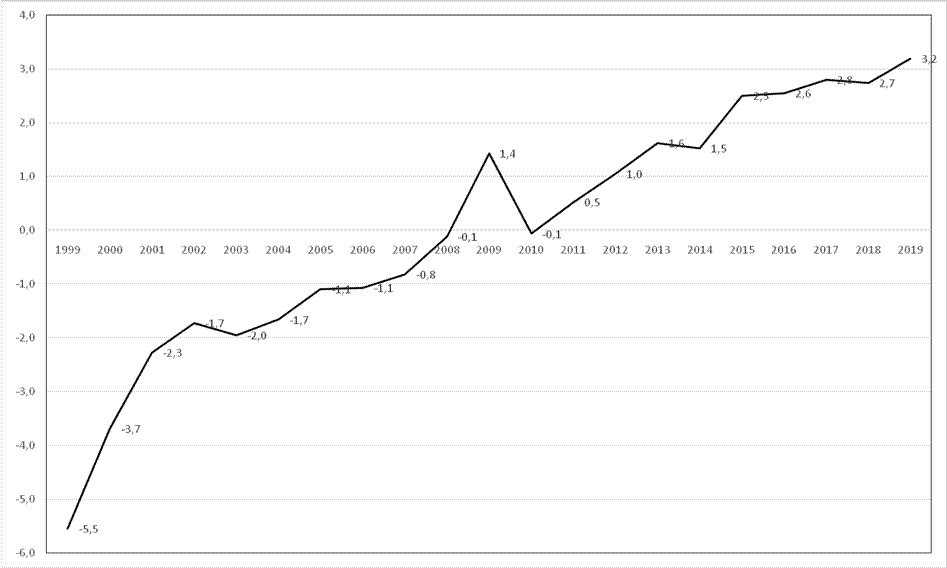
Рисунок 3. Величина счетов по первой главной компоненте

Источник: рассчитано автором на основе данных Федеральной службы государственной статистики.

Изучение графика счетов позволяет сделать вывод о поступательном развитии экономики России. В соответствии с теорией экономических циклов присутствуют колебания. На смену пикам экономического роста в 2002, 2005, 2009, 2015 годах приходят падения в 2003, 2010 и 2014 годах.

По результатам применения регрессии на главные компоненты построена следующая регрессионная модель:

у=0,03*х₁+0,2*х₂+0,1*х₃-0,07*х₄+0,2*х₅+0,6*х₆+0,2*х₇-0,0000002*х₈-0,0001*х₉ -60,573963 (9)

Для оценки адекватности построенной модели был рассчитан коэффициент детерминации. Его значение составило 0,8: построенная модель объясняет 80% колебаний результирующего фактора, а следовательно, приемлема для анализа. На рисунке 4 представлена динамика исходных значений результирующего показателя и динамика значений, рассчитанных на основе модели (9).

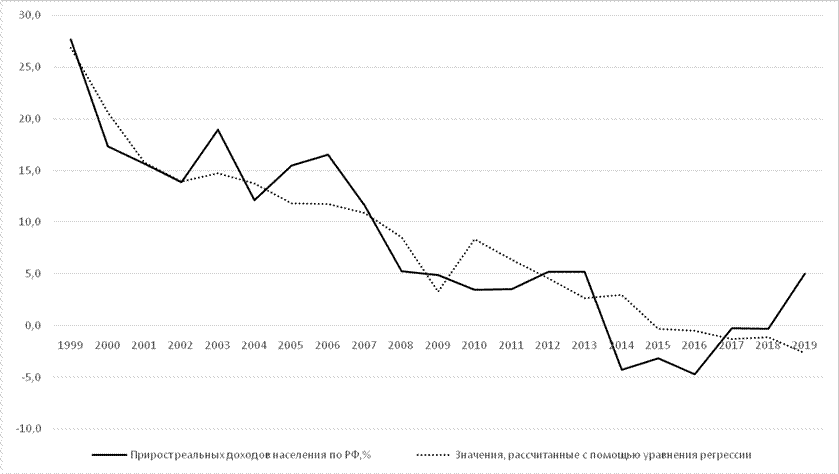
Рисунок 4. Исходные и выровненные с помощью модели значения

Источник: рассчитано автором на основе данных Федеральной службы государственной статистики.

Модель позволяет прогнозировать общие тенденции изменения прироста реальных доходов населения. Поэтому ее можно рекомендовать для оценки спроса на инновационный продукт на начальных этапах разработки проекта.

Заключение

Решению актуальной проблемы оценки спроса на инновации посвящено множество исследований. В случае повышения достоверности прогноза можно ожидать роста инновационной активности, так как в этом случае риски по инновационному проекту снижаются.

Проблема оценки спроса на инновационные товары может быть решена на основе моделирования прироста реальных доходов населения. В качестве регрессионной модели применена модель регрессии на главные компоненты. По результатам моделирования выявлена главная компонента, влияющая на прирост реальных доходов населения. Это фактор цикличности экономической системы. Построенная модель является адекватной и может быть использована для прогнозирования. В результате спрос на инновационный продукт можно оценить на основе прогнозов по ставке рефинансирования, уровню инфляции, уровню безработицы, величине инвестиций.

[1] Условные обозначения указаны в таблице 1.

[2] В скобках приведены значения нагрузок.