Принцип многокритериального ранжирования экономических систем

Лапаев Д.Н.¹
¹ Нижегородский государственный технический университет им. Р.Е. Алексеева, Нижний Новгород, Россия

Статья в журнале

Креативная экономика ^{(РИНЦ, ВАК)}
опубликовать статью | оформить подписку

Том 20, Номер 2 (Февраль 2026)

Аннотация:
Взаимосвязанные вопросы устойчивого развития, экономической безопасности, научно-технологического прогресса и роста экономики широко обсуждаются в научной литературе. При этом сравнительный анализ экономических систем различных иерархических уровней, как правило, осуществляется в многокритериальной либо многопроекционной постановке. Базовые методы и модели такого выбора известны и получили значительное развитие в последние годы. На фоне этого отчетливо проявилось отставание концептуальных положений и принципов. Частичному исправлению ситуации служит данная статья. Излагаемый в работе принцип ранжирования предусматривает каскадное выделение второго и нижестоящих рангов путем применения к оставшимся альтернативам (остатку) классического принципа Парето. Сокращаемый по мере исследования остаток представляет собой разность между исходным множеством систем и всеми множествами вышестоящих рангов. По результатам ряда итераций синтезируется ранговая структура в логике от лучших систем к худшим. Принцип ранжирования органично дополнит систему принципов многокритериальной и многопроекционной оптимизации в экономике и будет востребован при формировании и развитии профильных подходов, методов, моделей и классификаций для исследования широкого спектра экономических систем на разных иерархических уровнях при решении ключевых задач оценки устойчивости, безопасности, инновационности и эффективности

Ключевые слова: экономическая безопасность, устойчивое развитие, экономическая система, многокритериальный выбор, сопоставление, эффективное множество, ранг, принцип Парето, принцип ранжирования

JEL-классификация: O10, C61, C65

JATS XML

Введение

Взаимосвязанные вопросы устойчивого развития, экономической безопасности, научно-технологического прогресса и роста экономики широко обсуждаются в профильной научной литературе [20, 22] (Sadovnichy [et al.], 2023; Gorodetsky [et al.], 2023) и многих других источниках. Важным компонентом такого рода исследований выступает осуществление межстрановых, страновых, региональных, отраслевых, муниципальных сопоставлений, равно как и сопоставление организаций, их подразделений, а также интегрированных структур. При этом сравнительный анализ экономических систем различных иерархических уровней, как правило, реализуются в многокритериальной либо многопроекционной постановке [3–5] (Lapaeva, 2015; Lapaeva, 2018; Lapaeva, 2017). Известно, что базис многокритериального выбора закладывает принцип Парето [19] (Pareto, 2018), предусматривающий нахождение эффективного множества (первого ранга), как совокупности взаимно несравнимых (неулучшаемых) экономических систем [21] (Danilov-Danilyan [et al.], 2003). При разделении показателей на группы (проекции) проводится многокритериальный анализ в проекциях, завершаемый синтезом многопроекционного решения. Разработанные 8-10 лет назад принципы многопроекционной оптимизации достаточно разнообразны [18] (Lapaeva, 2017). Они учитывают жесткость и мягкость выбора [9, 13, 17] (Lapaeva, 2015; Lapaeva, 2015; Lapaeva, 2015), интересы стейкхолдеров [7, 11, 15] (Lapaeva, 2016; Lapaeva, 2015; Lapaeva, 2015), прогнозные сведения [6, 8, 10, 12, 14, 16] (Lapaeva, 2017; Lapaeva, 2016; Lapaeva, 2016; Lapaeva, 2016; Lapaeva, 2017; Lapaeva, 2016), иные аспекты, что позволяет генерировать широкий круг решений в виде кластера. Однако все упомянутые принципы никак не регламентируют процесс дальнейшего иерархического синтеза ранговой/кластерной структуры сравниваемых экономических систем по мере ухудшения положения последних, дающей исчерпывающую информацию о происходящих явлениях и процессах. Базовые принципы явно не отвечают актуальным запросам экономической науки и практики, отчетливо отставая от развития профильных методов и моделей [1, 2] (Lapaev, 2025; Lapaev, 2025). Частичному восполнению этого пробела служит данная статья.

Основная часть

Предлагаемый в статье принцип ранжирования предусматривает каскадное выделение второго и нижестоящих рангов путем применения к оставшимся альтернативам (остатку) классического принципа Парето. Сокращаемый по мере исследования остаток представляет собой разность между исходным множеством систем и всеми множествами вышестоящих рангов. Остатком для построения второго ранга выступает так называемое неэффективное множество, т.е. исходное множество систем за исключением эффективных альтернатив (вариантов первого ранга, иными словами – протоструктуры). Остатком для выделения третьего ранга служит исходное множество систем с удаленными элементами первого и второго рангов и т.д. По результатам ряда итераций формируется полная (или усеченная) ранговая структура в логике от лучших систем к худшим.

Для пояснения сущности принципа ранжирования рассмотрим пример выделения ранговой структуры при сопоставлении экономических систем S₁–S₁₀ по трем показателям К₁–К₃ в восьми ситуациях.

Ситуация 1

Все показатели требуется максимизировать.

Построение эффективного множества начнем с формирования сортированного массива. Для этого упорядочим по мере возрастания значений показателей номера 1–10 сравниваемых экономических систем. Здесь и далее в массивах эффективные варианты выделены жирным шрифтом.

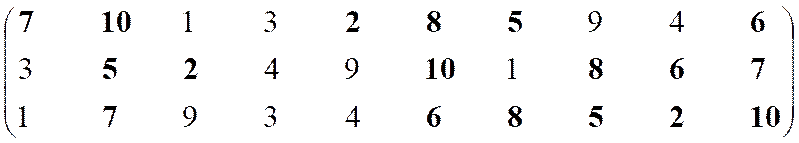
Неэффективны (слева от оптимумов)	Эффективны (крайние правые системы)
1, 3, 4, 9	6
–	7
–	10
Остаток 2, 5, 8 (несравнимы)	Решение 2, 5, 6, 7, 8, 10

Множество эффективных экономических систем запишем в виде М_эф = {S₂, S₅, S₆, S₇, S₈, S₁₀}. Дальнейшему анализу подлежат альтернативы S₁, S₃, S₄ и S₉.

Построение множества второго ранга.

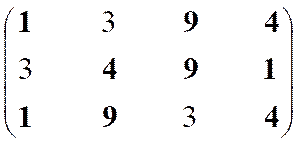
Неоптимальны (слева от оптимумов)	Оптимальны (крайние правые системы)
3	4
–	1
Остаток 9	Решение 1, 4, 9

Следовательно, множество систем второго ранга примет вид М_2р = {S₁, S₄, S₉}. Оптимальные варианты выделены жирным шрифтом в массивах. Альтернатива S₃ составит заключительный третий ранг.

Структура включает три ранга: первый ранг (протоструктура) представлен шестью экономическими системами, второй – тремя и третий – одной.

Ситуация 2

Необходимо минимизировать показатели К₁ и К₂ и максимизировать показатель К₃. Поменяем в первой и второй строках порядок следования номеров на обратный.

Формирование эффективного множества.

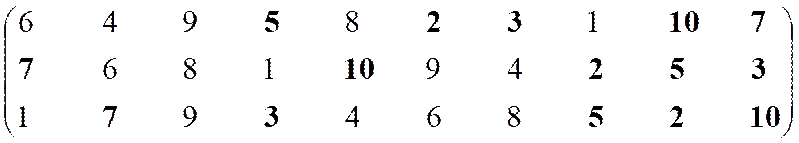
Неэффективны	Эффективны
–	7
9	3
1, 6, 8	10
Остаток 2, 4, 5

Среди них доминируем вариант S₄. Множество эффективных систем запишем в виде М_эф = {S₂, S₃, S₅, S₇, S₁₀}. Дальнейшему анализу подлежат альтернативы S₁, S₄, S₆, S₈ и S₉.

Построение множества второго ранга.

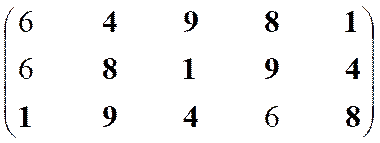
Неоптимальны	Оптимальны
–	1
–	4
6	8
Остаток 9	Решение 1, 4, 8, 9

Множество систем второго ранга примет вид М_2р = {S₁, S₄, S₈, S₉}. Альтернатива S₆ составит заключительный третий ранг.

Структура включает три ранга: первый ранг представлен пятью экономическими системами, второй – четырьмя, а третий – одной.

Ситуация 3

Требуется минимизировать показатель К₁ и максимизировать показатели К₂ и К₃. Сообразно этому перестраиваем матрицу эффективности.

Формирование эффективного множества.

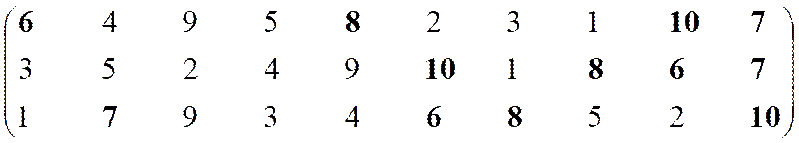
Неэффективны	Эффективны
1	7
2–5, 9	10
Остаток 6, 8 (несравнимы)	Решение 6, 7, 8, 10

Множество эффективных систем – М_эф = {S₆, S₇, S₈, S₁₀}, поэтому дальнейшему анализу подлежат альтернативы S₁–S₅ и S₉.

Построение множества второго ранга, итерация 1.

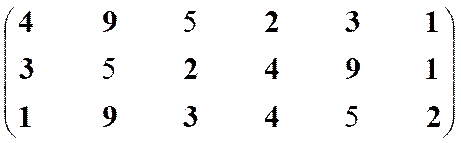
Неоптимальны	Оптимальны
–	1
5	2
Остаток 3, 4, 9 (несравнимы)	Решение 1, 2, 3, 4, 9

Множество второго ранга примет вид М_2р = {S₁, S₂, S₃, S₄, S₉}. Альтернатива S₅ составит заключительный третий ранг.

Структура включает три ранга: первый ранг представлен четырьмя экономическими системами, второй – пятью, а третий – одной.

Ситуация 4

Необходимо максимизировать показатели К₁ и К₃ и минимизировать показатель К₂. Корректируем матрицу.

Формирование эффективного множества, итерация 1.

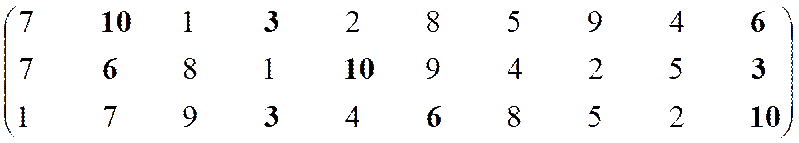
Неэффективны	Эффективны
7	6
1, 7	3
7	10
Остаток 2, 4, 5, 8, 9

Итерация 2.

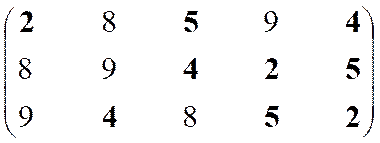
Неэффективны	Эффективны
9	4
8	5
	2
	Решение 2, 3, 4, 5, 6, 10

Множество эффективных систем – М_эф = {S₂, S₃, S₄, S₅, S₆, S₁₀}, тогда дальнейшему анализу подлежат альтернативы S₁ и S₇–S₉.

Построение множества второго ранга.

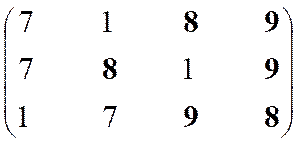
Неоптимальны	Оптимальны
1, 7	9
	8
	Решение 8, 9

Тогда множество систем второго ранга примет вид М_2р = {S₈, S₉}. Взаимно несравнимые варианты S₁ и S₇ составят заключительный третий ранг.

Структура включает три ранга: первый ранг представлен шестью экономическими системами, а второй и третий ранги – двумя.

Ситуация 5

Требуется максимизировать показатели К₁ и К₂ и минимизировать показатель К₃. Перестраиваем матрицу.

Формирование эффективного множества.

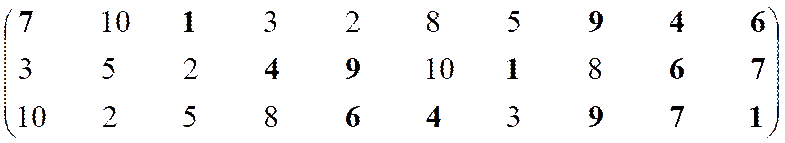
Неэффективны	Эффективны
2, 5, 8, 10	6
–	7
10	1
Остаток 3, 4, 9

Среди них доминируем вариант S₃. Множество эффективных систем – М_эф = {S₁, S₄, S₆, S₇, S₉}. Дальнейшему анализу подлежат альтернативы S₂, S₃, S₅, S₈ и S₁₀.

Построение множества второго ранга.

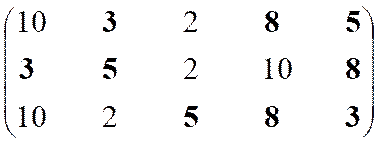
Неоптимальны	Оптимальны
–	5
2, 10	8
	3
	Решение 3, 5, 8

Таким образом, множество систем второго ранга примет вид М_2р = {S₃, S₅, S₈}. Взаимно несравнимые варианты S₂ и S₁₀ составят заключительный третий ранг.

Структура включает три ранга: первый ранг представлен пятью экономическими системами, второй – тремя и третий – двумя.

Ситуация 6

Все показатели необходимо минимизировать. Корректируем матрицу.

Формирование эффективного множества.

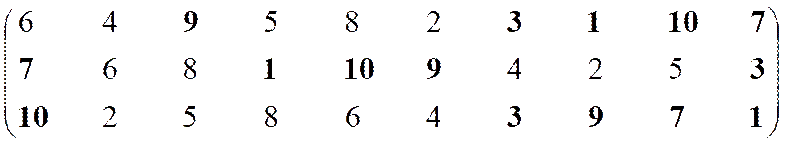
Неэффективны	Эффективны
–	7
2, 4–6, 8	3
6, 8	1
Остаток 9, 10 (несравнимы)	Решение 1, 3, 7, 9, 10

Множество эффективных систем – М_эф = {S₁, S₃, S₇, S₉, S₁₀}, тогда дальнейшему анализу подлежат альтернативы S₂, S₄–S₆ и S₈.

Построение множества второго ранга.

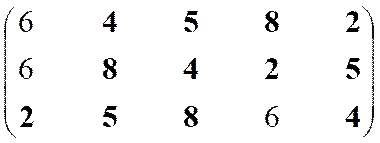
Неэффективны	Эффективны
–	2
–	5
6	4
Остаток 8	Решение 2, 4, 5, 8

При этом множество систем второго ранга примет вид М_2р = {S₂, S₄, S₅, S₈}. Вариант S₆ составит заключительный третий ранг.

Структура включает три ранга: первый ранг представлен пятью экономическими системами, второй – четырьмя и третий – одной.

Ситуация 7

Требуется минимизировать показатели К₁ и К₃ и максимизировать показатель К₂. Перестраиваем массив.

Формирование эффективного множества.

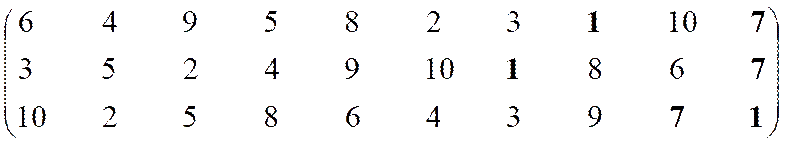
Неэффективны	Эффективны
2–6, 8–10	7
	1
	Решение 1, 7

Множество эффективных систем – М_эф = {S₁, S₇}, поэтому дальнейшему анализу подлежат альтернативы S₂–S₆ и S₈–S₁₀.

Построение множества второго ранга, итерация 1.

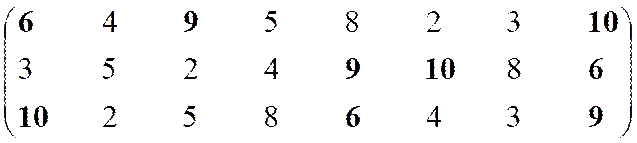
Неоптимальны	Оптимальны
–	10
–	6
4	9
Остаток 2, 3, 5, 8

Итерация 2.

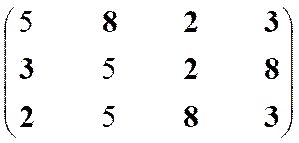
Неоптимальны	Оптимальны
–	3
5	8
Остаток 2	Решение 2, 3, 6, 8, 9, 10

Множество систем второго ранга примет вид М_2р = {S₂, S₃, S₆, S₈, S₉, S₁₀}. Взаимно несравнимые варианты S₄ и S₅ составят заключительный третий ранг.

Структура включает три ранга: первый и последний ранги представлены двумя экономическими системами, а второй – шестью.

Ситуация 8

Необходимо максимизировать показатель К₁ и минимизировать показатели К₂ и К₃. Корректируем массив.

Формирование эффективного множества, итерация 1.

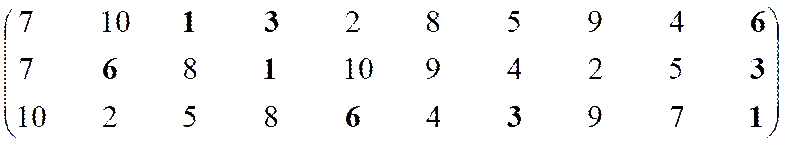
Неэффективны	Эффективны
–	6
10	3
7	1
Остаток 2, 4, 5, 8, 9

Итерация 2.

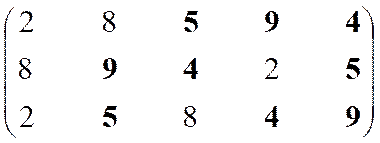
Неэффективны	Эффективны
8	4
2	5
	9
	Решение 1, 3, 4, 5, 6, 9

Множество эффективных систем – М_эф = {S₁, S₃, S₄, S₅, S₆, S₉}, тогда дальнейшему анализу подлежат альтернативы S₂, S₇, S₈ и S₁₀.

Построение множества второго ранга.

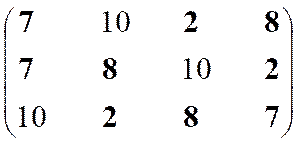
Неэффективны	Эффективны
–	8
10	2
	7
	Решение 2, 7, 8

Таким образом, множество вариантов второго ранга примет вид М_2р = {S₂, S₇, S₈}. Альтернатива S₁₀ составит заключительный третий ранг.

Структура включает два ранга: первый ранг представлен шестью экономическими системами, второй – тремя и третий – одной. Суть принципа ясна.

Заключение

Принцип ранжирования органично дополнит исходную систему принципов многокритериальной и многопроекционной оптимизации в экономике и будет востребован при формировании и развитии профильных подходов, методов, моделей и классификаций для исследования широкого спектра экономических систем на разных иерархических уровнях при решении ключевых задач оценки устойчивости, безопасности, инновационности и эффективности.

Источники:

1. Лапаев Д.Н. Система методов многокритериального и многопроекционного выбора в экономике // Развитие и безопасность. – 2025. – № 2. – c. 58-69.
2. Лапаев Д.Н. Система моделей многокритериального и многопроекционного выбора в экономике // Вестник Самарского университета. Экономика и управление. – 2025. – № 2. – c. 21-31. – doi: 10.18287/2542-0461-2025-16-2-21-31.
3. Лапаева О.Н. Многокритериальная оценка экономического состояния предприятий и отраслей промышленности и выбор предпочтительных альтернатив. / Монография. - Нижний Новгород: НГТУ, 2015. – 145 c.
4. Лапаева О.Н. Многопроекционная оценка состояния промышленных экономических систем. / Монография. - Нижний Новгород: НГТУ, 2018. – 371 c.
5. Лапаева О.Н. Многопроекционная сравнительная оценка альтернатив в экономике. / Монография. - Нижний Новгород: НГТУ, 2017. – 210 c.
6. Лапаева О.Н. Принцип ранжированного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1. – c. 105-108.
7. Лапаева О.Н. Принцип ранжированного выбора взаимоприемлемого многопроекционного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2016. – № 6. – c. 128-131.
8. Лапаева О.Н. Принцип ранжированного выбора многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2016. – № 9-3. – c. 157-159.
9. Лапаева О.Н. Принцип ранжированного выбора многопроекционного решения // Экономика, статистика и информатика. Вестник УМО. – 2015. – № 3. – c. 192-195.
10. Лапаева О.Н. Принцип точечного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2016. – № 9-3. – c. 160-163.
11. Лапаева О.Н. Принцип точечного выбора взаимоприемлемого многопроекционного решения // Экономика, статистика и информатика. Вестник УМО. – 2015. – № 4. – c. 134-137.
12. Лапаева О.Н. Принцип точечного выбора многопроекционного прогнозного решени // Экономика, статистика и информатика. Вестник УМО. – 2016. – № 1. – c. 10-13.
13. Лапаева О.Н. Принцип точечного выбора многопроекционного решения // Экономика, статистика и информатика. Вестник УМО. – 2015. – № 1. – c. 78-81.
14. Лапаева О.Н. Принцип эффективного выбора взаимоприемлемого многопроекционного прогнозного решения // Конкурентоспособность в глобальном мире: экономика, наука, технологии. – 2017. – № 1-1. – c. 102-104.
15. Лапаева О.Н. Принцип эффективного выбора взаимоприемлемого многопроекционного решения // Экономика, статистика и информатика. Вестник УМО. – 2015. – № 5. – c. 105-107.
16. Лапаева О.Н. Принцип эффективного выбора многопроекционного прогнозного решения // Экономика, статистика и информатика. Вестник УМО. – 2016. – № 2. – c. 45-47.
17. Лапаева О.Н. Принцип эффективного выбора многопроекционного решения // Экономика, статистика и информатика. Вестник УМО. – 2015. – № 2. – c. 83-85.
18. Лапаева О.Н. 3.5 Принципы сравнительной оценки альтернатив в экономике по совокупности проекций // Аудит и финансовый анализ. – 2017. – № 1. – c. 106-109.
19. Парето В. Учебник политической экономии. / [пер. с франц.], 2-е изд. - М.: РИОР: ИНФРА-М, 2018. – 591 c.
20. Садовничий В.А. Преодолевая пределы роста. Основные положения доклада для Римского клуба. / Монография. - М.: МГУ, 2023. – 99 c.
21. Данилов-Данильян В. И. Экономико-математический энциклопедический словарь. - М.: ИНФРА-М, 200. – 687 c.
22. Городецкий А. Е. Экономическая безопасность России: теоретическое обоснование и методы регулирования. / Монография. - М.: Институт экономики РАН, 2023. – 361 c.

Страница обновлена: 19.02.2026 в 22:16:22

The principle of multi-criteria ranking of economic systems

Lapaev D.N.

Journal paper

Creative Economy
Volume 20, Number 2 (February 2026)

Citation:

Abstract:
The interrelated issues of sustainable development, economic security, scientific and technological progress, and economic growth are widely discussed in the scientific literature. In this context, a comparative analysis of economic systems at various hierarchical levels is typically conducted using multi-criteria or multi-projection approaches. The basic methods and models for such selection are well-known and have undergone significant development in recent years. However, there has been a noticeable gap in the conceptual framework and principles. The article aims to address this issue. The ranking principle described in the article involves cascading the selection of the second and lower ranks by applying the classical Pareto principle to the remaining alternatives (the remainder). The remainder, which is reduced as the research progresses, is the difference between the initial set of systems and all the sets of higher ranks. After a series of iterations, a rank structure is synthesized in the logic of best to worst systems. The principle of ranking will seamlessly complement the system of principles for multi-criteria and multi-projection optimization in economics and will be relevant in the development of specialized approaches, methods, models, and classifications for studying a wide range of economic systems at different hierarchical levels in order to address key issues related to sustainability, security, innovation, and efficiency.

Keywords: economic security, sustainable development, economic system, multi-criteria selection, comparison, effective set, rank, Pareto principle, ranking principle

JEL-classification: O10, C61, C65

References:

Danilov-Danilyan V. I. (200). Economic and mathematical encyclopedic dictionary

Gorodetskiy A. E. (2023). Economic security of Russia: theoretical justification and methods of regulation

Lapaev D.N. (2025). A system of models of multi-criteria and multi-projection choice in economics. Vestnik Samarskogo universiteta. Ekonomika i upravlenie. 16 (2). 21-31. doi: 10.18287/2542-0461-2025-16-2-21-31.

Lapaev D.N. (2025). System of Methods of Multicriteria and Multi-projection Choice in Economics. Razvitie i bezopasnost. (2). 58-69.

Lapaeva O.N. (2015). Principle of Effective Making of Multi-projection Decision. Statistics and Economics. (2). 83-85.

Lapaeva O.N. (2015). Principle of Effective Making of Mutually Acceptable Multi-projection Decision. Statistics and Economics. (5). 105-107.

Lapaeva O.N. (2015). Principle of Point Making of Multi-projection Decision. Statistics and Economics. (1). 78-81.

Lapaeva O.N. (2015). Principle of Ranking Making of Multi-projection Decision. Statistics and Economics. (3). 192-195.

Lapaeva O.N. (2015). Principle of Point Making of Mutually Acceptable Multiprojection Decision. Statistics and Economics. (4). 134-137.

Lapaeva O.N. (2015). Multi-criteria assessment of the economic condition of enterprises and industries and selection of preferred alternatives

Lapaeva O.N. (2016). Principle of Effective Making of Multi-projection Predictive Decision. Statistics and Economics. (2). 45-47.

Lapaeva O.N. (2016). Principle of Point Making of Multi-projection Predictive Decision. Statistics and Economics. (1). 10-13.

Lapaeva O.N. (2016). The principle of a ranked choice of a mutually acceptable multi-projection solution. Competitiveness in the global world: economy, science, technology. (6). 128-131.

Lapaeva O.N. (2016). The principle of point selection of a mutually acceptable multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (9-3). 160-163.

Lapaeva O.N. (2016). The principle of ranked selection of a multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (9-3). 157-159.

Lapaeva O.N. (2017). 3.5. Principles of Comparative Evaluation of Alternatives in Economics by a Set of Projections. Audit and financial analysis. (1). 106-109.

Lapaeva O.N. (2017). The principle of a ranked choice of a mutually acceptable multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (1-1). 105-108.

Lapaeva O.N. (2017). The principle of effective selection of a mutually acceptable multi-projection predictive solution. Competitiveness in the global world: economy, science, technology. (1-1). 102-104.

Lapaeva O.N. (2017). A multi-projection comparative assessment of alternatives in the economy

Lapaeva O.N. (2018). Multi-projection assessment of the state of industrial economic systems

Pareto V. (2018). Textbook of Political Economics

Sadovnichiy V.A. (2023). Overcoming the limits of growth. The main provisions of the report for the Club of Rome

Подробнее об авторах:

The principle of multi-criteria ranking of economic systems