Экономическая сущность критериев оптимальности при проектировании несущих конструкций в условиях обеспечения эффективности капитальных вложений

Введение

Сложившаяся исторически парадигма проектирования строительных конструкций основывалась на принципах, унаследованных из классической механики, где доминирующим критерием выступала минимизация массы. Такой подход был обусловлен объективными факторами, во-первых, экономического характера — дефицитом и высокой стоимостью материалов, во-вторых, ограниченными возможностями вычислительной техники, не позволявшей осуществлять сложные экономические расчеты. Однако по мере развития мировой экономики, глобализации логистических цепочек, совершенствования производственных технологий и усложнения строительных систем возникла настоятельная потребность в пересмотре системы оценочных показателей оптимальности несущих строительных систем. В современных исследованиях отмечается устойчивая тенденция к формированию новых, более комплексных критериев оптимальности, которые должны интегрировать не только технические, но и экономические, экологические и социальные аспекты, отражая прикладной характер решаемых задач.

Актуальность настоящего исследования для экономической науки определяется тем, что выбор критерия оптимальности непосредственно влияет на капиталоемкость строительного проекта, его будущие эксплуатационные расходы и, в конечном счете, на общую экономическую эффективность инвестиций. Это положение отмечалось в работах многих исследователей, в том числе в работах Е.Л. Богдановой, К.А. Соловейчик, К.Г. Аркиной [2], Ю.М. Вайвера [3], В.В. Крылова [5], А.О. Куликова [6], О.А. Тупиковой, Т.А. Беккер, М.В. Бузиной [10] и др. Однако до сих пор проблемным вопросом остается недостаточный учет критерия оптимальности экономического характера при выборе конструкции объекта, так как не всегда принятие технически рационального решения на стадии проектирования, обосновано экономически, что сказывается на росте затрат по проекту, увеличение его конечно стоимости и инвестиционной эффективности в целом. Таким образом, цель исследования состоит в обосновании целесообразности применения критериев оптимальности строительных несущих систем с акцентом на методологию построения и применения комплексных стоимостных моделей, что в условиях достижения эффективности капиталовложений позволит принимать управленческие решения относительно реализации проекта не только с позиции технически рационального решения, но и позиции экономической эффективности этого решения. систематизации и углубленном анализе экономической

Методология

Формирование авторской позиции относительно экономической сущности критериев оптимальности несущих строительных систем основано, в первую очередь, на ретроспективном анализе развития критериев оптимальности от механических к экономическим показателям:

1. Период технико-механического доминирования. На начальном этапе развития теории оптимизации в строительстве преобладающим критерием являлась минимизация массы конструкции. Этот показатель был интуитивно понятен, поскольку напрямую связан с трудоемкостью обработки материалов, сложностью транспортировки и монтажа несущих систем. Одним из наиболее эффективных методов решения задач минимизации массы для металлических конструкций признан метод характеристик нагрузки, разработанный выдающимся советским ученым Н.С. Стрелецким [8]. Данная методика позволяла формализовать процесс определения минимально необходимых сечений элементов при заданных нагрузках и условиях эксплуатации. Существенный вклад в развитие теоретической базы вариантного проектирования внес Я.М. Лихтарников. В своих научных трудах он сформулировал три основных критерия, по которым можно было осуществлять оптимизацию в рамках решения однокритериальных задач — это прочность, экономичность и технологичность. На этом этапе произошло осознание того, что критерий минимизации массы не является объективным. Использование предложенных трех критериев на примере решения задач для стальных конструкций показало необходимость и заложило основы использования экономических критериев и стоимостного подхода к оценке рациональности конструктивных решений в условиях необходимости обеспечения эффективности капиталовложений [1,9].

2. Формирование и развитие стоимостного подхода. Методологический опыт, накопленный отечественной научной школой при оптимизации стальных конструкций, впоследствии был успешно адаптирован для железобетонных несущих систем. Однако применение критерия минимума стоимости к железобетону выявило его значительно более сложную экономическую природу по сравнению со стальными конструкциями. В современной мировой строительной науке и практике произошел качественный переход: стоимостной критерий перестал рассматриваться как простая сумма затрат на материалы и монтаж [4]. В настоящее время он анализируется в контексте полного жизненного цикла объекта (Life Cycle Costing). Этот подход предполагает учет всех затрат, возникающих на различных этапах существования сооружения: проектирование, строительство, эксплуатация (включая техническое обслуживание и ремонты), возможная реконструкция и, наконец, утилизация. Такой комплексный подход позволяет дать объективную оценку экономической эффективности проекта в долгосрочной перспективе.

Следует отметить, что сейчас в отдельных случаях может быть применен критерий минимизации массы или материалоемкости. Это происходит, если производство конструкций и стройка находятся в непосредственной близости и используются местные строительные материалы. Главным условием при этом является стоимость материалов и услуг, которая должна быть относительно стабильной и предсказуемой.

Основная часть

1. Обоснование объективности стоимостного критерия для оптимизации несущих конструкций. При однокритериальной оптимизации стальных, железобетонных, деревянных и других несущих конструкций в отечественной практике используется критерий минимизации стоимости «в деле», то есть стоимости готовой к эксплуатации конструкции, возведенной на строительной площадке. Определяющая роль этого критерия обусловлена комплексом фундаментальных свойств строительной продукции, которые невозможно адекватно учесть только путем оценки расхода материалов. Детальный анализ этих свойств позволяет выделить следующие ключевые аспекты:

а) существенная дифференциация ресурсов по стоимости и доступности. Конструкция состоит из двух принципиально различных материалов – бетона и стальной арматуры. Эти материалы имеют разную сырьевую базу, технологии производства и, как следствие, различную территориальную доступность и рыночную конъюнктуру. Цены на цемент, заполнители, стальную арматуру могут изменяться асинхронно и демонстрировать ярко выраженную региональную специфику. Например, в регионах, богатых месторождениями цементного сырья, стоимость бетона может быть на 25-40% ниже, чем в регионах, куда все компоненты необходимо завозить. Этот аспект иллюстрируется рисунках 1,2.

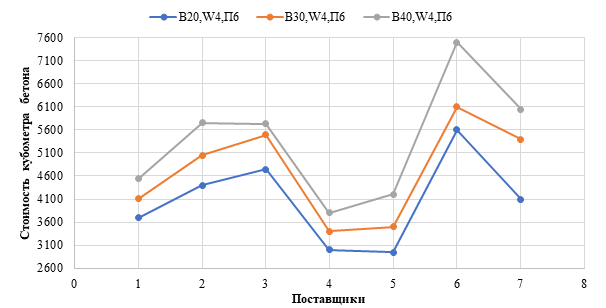
Рисунок 1 – Изменение стоимости бетона различных классов у различных поставщиков: 1 – Москва; 2 – Нижний Новгород; 3 – Саратов; 4 – Ростов-на-Дону; 5 – Челябинск; 6 – Нижневартовск; 7 – Хабаровск;

B20,W4,П6; B30,W4,П6; B40,W4,П6 – классы бетонов (составлен авторами на основе данных аналитического портала «Мониторинг цен» [7] информации из открытых источников)

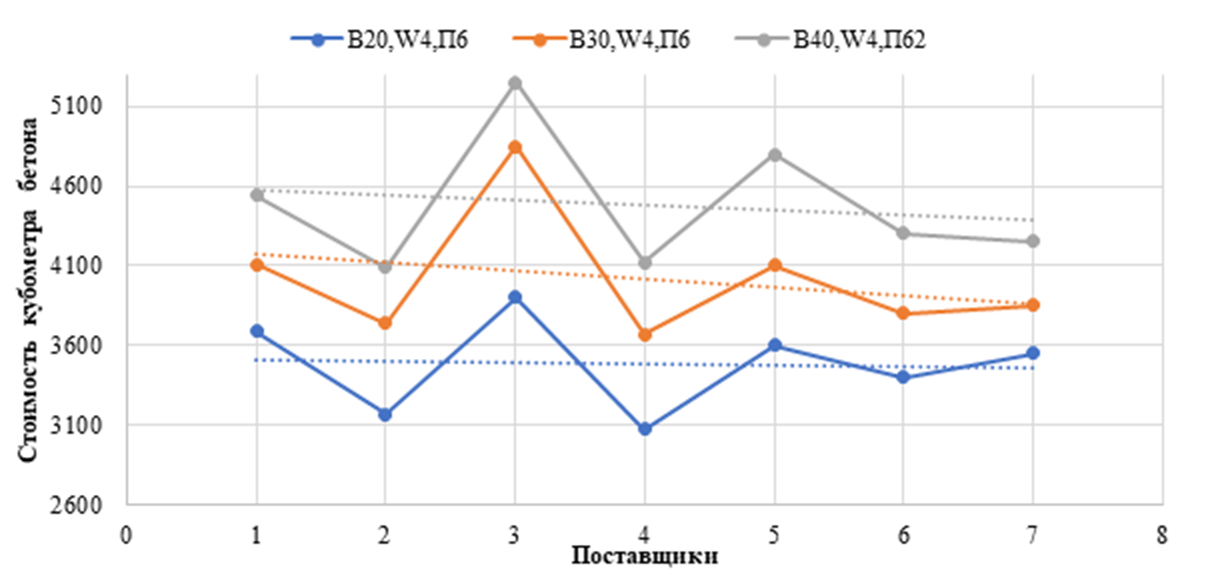
Рисунок 2 – Стоимость бетона в Москве и городах Московской области:1 – Москва; 2 – Подольск; 3 – Реутов; 4 – Пушкино; 5 – Мытищи; 6 – Электросталь; 7 – Люберцы; B20,W4,П6; B30,W4,П6; B40,W4,П6 – классы бетонов (составлен авторами на основе данных аналитического портала «Мониторинг цен» [7])

Как видно из рисунков 1 и 2 динамика стоимостей бетона существенно различна даже в пределах одной области. Из-за относительно высокой волатильности рынка строительных материалов в критериях оптимизации могут учитываться отношения стоимостей. Например, для железобетонных конструкций это величина (П) отношения стоимости арматуры к бетону:

(1),

где C_s – стоимость арматуры;

C_b – стоимость бетона.

Для этой величины можно проследить динамику стоимости материалов (рисунок 3,4).

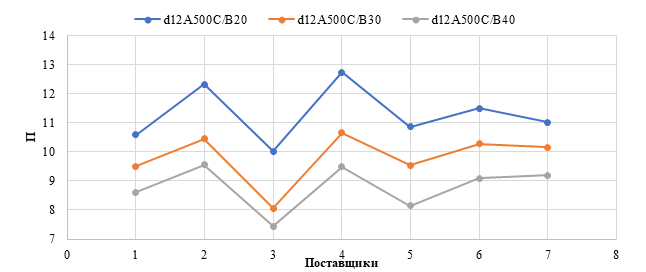
Рисунок 3 – Изменение величины П по Москве и московской области: 1 – Москва; 2 – Подольск; 3 – Реутов; 4 – Пушкино; 5 – Мытищи; 6 – Электросталь; 7 – Люберцы; d12A500C/B20; d12A500C/B30; d12A500C/B40– классы железобетонных конструкций (составлен авторами на основе данных аналитического портала «Мониторинг цен» [7])

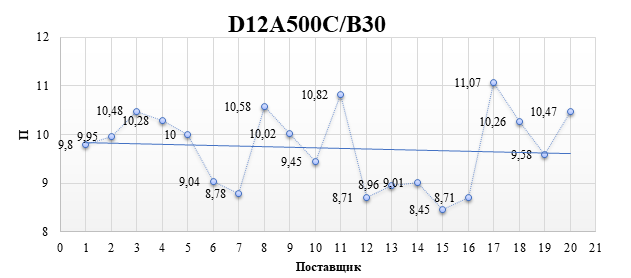
Рисунок 4 – Изменение параметра П в г. Москва: 1-20 номера поставщиков строительных материалов (составлен авторами на основе данных аналитического портала «Мониторинг цен» [7])

б) Принципиальные различия в технологиях изготовления. Различные конструктивные и технологические решения существенно различаются по трудоемкости, уровню механовооруженности, энергоемкости и, соответственно, по структуре затрат на их производство, что, в свою очередь, влияет на инвестиционную эффективность. Сборное производство требует значительных капитальных вложений в заводскую инфраструктуру, но позволяет существенно снизить затраты и сроки на строительной площадке. Монолитное строительство характеризуется повышенными затратами на организацию работ на площадке, но обеспечивает высокие механические характеристики. Это, в свою очередь, также влияет на требования к грузоподъемной технике, квалификации рабочих, организации строительной площадки, что непосредственно влияет на стоимость подрядных работ и конечную стоимость проекта.

в) многофакторность ценообразования в условиях рыночной экономики. Стоимость конструкции формируется под влиянием множества рыночных факторов, которые не являются стабильными. Среди них можно выделить: логистические издержки – удаленность поставщиков от строительной площадки, тарифы на перевозки, наличие транспортной инфраструктуры; наличие местных ресурсов и производственных мощностей, объемы спроса и сезонные колебания конъюнктуры, уровень конкуренции среди поставщиков материалов и подрядных организаций.

Практика решения оптимизационных задач показала, что не принятие во внимание стоимостных факторов, определяемых вышеперечисленными особенностями, может привести к получению конструктивного решения, которое будет оптимальным с точки зрения прочности, жесткости и устойчивости и даже расхода материалов, но не будет являться экономически оптимальным и эффективным [1]. Его итоговая стоимость, включающая затраты на производство, транспортировку и монтаж, может оказаться выше, чем у альтернативного варианта с бóльшим расходом материалов, но с более низкими удельными затратами. Наглядным примером служит упомянутая выше региональная дифференциация цен на бетон (рисунок 1-2).

2. Многокритериальная оптимизация и применение методов теории игр в проектировании. Современные требования к строительным конструкциям отличаются комплексным характером и предполагают их проектирование с учетом взаимосвязанных и зачастую противоречивых критериев: оптимальности, экологических стандартов (включая снижение углеродного следа), безопасности, надежности, долговечности, пожарной устойчивости, влияния на комфорт внутренней среды. Очевидно, что ни одна конструкция не может быть одновременно оптимальной по всем перечисленным параметрам. Улучшение одного показателя (например, надежности) практически всегда достигается за счет ухудшения другого (например, стоимости). В этой связи возникает задача многокритериальной оптимизации, целью которой является не поиск единственного «абсолютно лучшего» решения, а определение множества Парето-оптимальных (неулучшаемых) решений. Парето-оптимальным называется такое решение, при котором любое изменение вектора проектных параметров не приводит к улучшению значения одного критерия без одновременного ухудшения значения хотя бы одного другого критерия. Иными словами, это решения, представляющие собой рациональный компромисс между конфликтующими целями [11].

Для несущих строительных конструкций в современных исследовательских практиках рассматривается широкий спектр целевых критериев, которые можно сгруппировать на экономические критерии, технико-эксплуатационные и экологические. К экономическим критериям, поиск значений которых сопровождается минимизацией целевой функции, относят стоимость материалов и изделий, стоимость монтажа или возведения (трудозатраты, трудоемкость, машиноемкость и др.), расходы на нормальную эксплуатацию (техническое обслуживание, текущие и капитальные ремонты), расходы на реконструкцию и техническое перевооружение, в т.ч. оценка потенциала повторного использования конструкций и материалов (их остаточной стоимости), стоимость жизненного цикла (LCC). К технико-эксплуатационным критериям относят обеспечение различных видов безопасности конструкций, зданий и сооружений в соответствии с нормативными требованиями и техническими регламентами; максимизацию долговечности, эксплуатационной надежности при установленном лимите затрат; обеспечение требуемого качества внутреннего пространства, для нормального хода функционального процесса в зданиях, например в показателях теплопроводности, звукоизоляции. К экологическим критериям относят углеродный след в процессе строительства, другие вредные выбросы в атмосферу; вредные воздействия, связанные с шумом, вибрацией и т.п. Многие из описанных критериев, объединяются в интегральный критерий LCC, который представляет собой дисконтированную сумму всех затрат, связанных с созданием, владением, использованием и ликвидацией объекта на протяжении всего периода его существования.

Для многокритериальной оптимизации решаемой задачи может применяться аппарат теории игр, а именно концепция равновесия Нэша. В контексте проектирования равновесие Нэша определяется как такая комбинация проектных параметров и ограничений задачи оптимизации, при которой удовлетворение ни одного из ограничений невозможно без изменения пороговых значений других ограничений. Применительно к стоимости несущей системы всего объекта такой подход можно распределить на участников строительства. Так, например, ни один из стейкхолдеров не может увеличить свою «полезность» (например, для инвестора – минимизация LCC, для подрядчика – максимизация прибыли), односторонне изменяя свою стратегию при условии, что остальные участники сохраняют свои стратегии неизменными [12].

В отличие от подхода Парето, который ориентирован на поиск технически эффективных решений, равновесие Нэша позволяет идентифицировать стратегически устойчивые решения, учитывающие меняющиеся условия эксплуатации, предпочтения и возможности всех заинтересованных сторон. Например, решение, оптимальное по Парето с точки зрения минимизации совокупной стоимости владения, может быть неприемлемо для подрядчика из-за низкой рентабельности и, следовательно, не будет реализовано. Методология равновесия Нэша позволяет найти взаимоприемлемый компромисс, увеличивающий вероятность успешной реализации проекта и эффективность капиталовложений.

3. Методология расчета интегрального стоимостного критерия оптимальности. Для практической реализации стоимостного подхода к оптимизации необходима детализированная математическая модель. При этом ее аналитическая формализация ввиду огромного числа варьируемых параметров невозможна. В этом случае используются эвристические методики, такие как генетические алгоритмы, методы роя частиц, отжига, эхолокации и др., однако для отдельных видов конструкций можно сформулировать аналитические функции. Для железобетонных конструкций стоимость можно получить путем

– коэффициенты удорожания работ в зимних условиях, и сложности (стесненности) работ;

– стоимость единицы объема бетона типа j , имеющего назначение i, определяемая для -го поставщика ;

– объем бетона;

– стоимость единицы массы арматуры класса l по прочности, имеющего назначение k, определяемая для -го поставщика ;

– масса арматуры;

С_q – размер основных затрат;

– размер дополнительных затрат;

– эксплуатационные затраты в период ;

– коэффициент, зависящий от уровня ответственности здания, для пониженного уровня , для нормального и повышенного уровней ;

– абсолютное значение риска последствий аварийной ситуации. Величина вычисляется:

– размер ущерба, соответствующий -той рисковой ситуации на -том периоде жизненного цикла сооружения [1,9].

Обращаясь к рисункам 1-4, отметим, что итоговая стоимость конструкции определяется не только физическим расходом материала, но и стратегическим выбором поставщика, логистической схемой и регионом строительства. Таким образом, при незначительно отличающейся итоговой стоимости можно получать конструкции с бóльшим (по сравнению с теоретическим минимумом) расходом материала. Более того, за те же деньги может быть назначен более высокий класс бетона по прочности или долговечности, что может положительно сказаться на надежности конструкции и привести к значительной экономии на эксплуатационных расходах в будущем.

Заключение

Проведенное исследование позволяет сделать вывод о том, что в условиях достижения эффективности капиталовложений для оптимизации строительных несущих систем с учетом стоимостных критериев необходимы эвристические методики и программные комплексы, позволяющие генерировать и анализировать широкий спектр альтернативных конструктивных решений при независимо варьируемых проектных и экономических параметрах. В результате проведенного исследования получено, что:

1. В условиях обеспечения эффективности капиталовложений критерий минимальной стоимости, особенно в его расширенной трактовке как стоимости жизненного цикла (LCC), является наиболее адекватным и универсальным критерием оптимальности для строительных конструкций. Он позволяет агрегировать разнородные факторы (материалы, технологию, логистику, риски, эксплуатацию) в едином измерителе.

2. Предложенная детализированная математическая модель расчета стоимостного критерия оптимальности железобетонных конструкций предоставляет практический инструмент для количественного сравнения различных проектных решений в условиях обеспечения эффективности капиталовложений. Ее ключевым преимуществом является гибкость и возможность адаптации к конкретным условиям проекта – от выбора местных поставщиков до учета специфических рисков.

3. В условиях, когда требуется одновременный учет нескольких конфликтующих целей (экономика, экология, безопасность), или ограничений (стоимость, прибыль, безопасность, надежность) оптимальной методологией является многокритериальная оптимизация с поиском множества Парето-оптимальных решений. Это позволяет лицу, принимающему решение (инвестору, заказчику), осознанно выбрать окончательный вариант из ряда рациональных компромиссов.

4. Введение критерия равновесия Нэша расширяет методологический аппарат, позволяя анализировать и разрешать математические коллизии и конфликт интересов между участниками проекта. Это переводит задачу из чисто инженерно-экономической в область стратегического управления проектом. Решение, устойчивое по Нэшу, имеет более высокие шансы на успешную реализацию, так как учитывает экономические мотивации всех сторон.

В качестве перспективных направлений дальнейших исследований следует рассмотреть возможность сочетания двух подходов – поиска множества Парето-оптимальных решений и последующего выбора среди них равновесия Нэша для проектов государственно-частного партнерства и крупных инфраструктурных объектов с множеством стейкхолдеров.