Алгоритмы градиентного бустинга против рекуррентных сетей в задачах прогнозирования
Жилина Е.В.1![]() , Ефимова Е.В.1
, Ефимова Е.В.1![]() , Тищенко Е.Н.1
, Тищенко Е.Н.1![]()
1 Ростовский государственный экономический университет (РИНХ), ,
Скачать PDF | Загрузок: 55
Статья в журнале
Информатизация в цифровой экономике (РИНЦ, ВАК)
опубликовать статью | оформить подписку
Том 6, Номер 1 (Январь-март 2025)
Эта статья проиндексирована РИНЦ, см. https://elibrary.ru/item.asp?id=81471903
Аннотация:
Сравнительный анализ методов машинного обучения и нейронных сетей является важным инструментом для выбора оптимальных решений, понимания их ограничений и возможностей, а также для развития новых подходов и технологий в области искусственного интеллекта; в ходе разработки решается задача прогнозирования временных рядов на основе показаний потребления электроэнергии; авторами разработаны алгоритмы прогнозирования данных с помощью методов машинного обучения (градиентный бустинг XGBoost, LightGBM и CatBoost, сравнение низкоуровневого и высокоуровневого интерфейсов xgb.train и XGBRegressor, SimpleLinearModel), а также с помощью нейронных сетей (рекуррентные сети, реализованные в Pytorch) на языке Python; для анализа и оценки полученных результатов были рассчитаны метрики качества моделей (RMSE ошибки обучения на тренировочных и тестовых данных), проведено комплексное сравнение алгоритмов (бенчмаркинг) на основе времени выполнения процесса обучения разработанных моделей; визуализированы прогнозные значения (реальные и расчетные).
Ключевые слова: Python, ML, XGBoost, LightGBM, CatBoost, xgb.train, SimpleLinearModel, нейронные сети, LSTM, Pytorch, бенчмаркинг
JEL-классификация: C40, C45, C49
Введение
Сравнительный анализ методов машинного обучения (ML) и нейронных сетей (НС) является важной задачей в современной аналитике и разработке интеллектуальных систем [10]. Актуальность обусловлена разнообразием решаемых типов задач (классификация, регрессия, кластеризация и т.д.) и сложностью алгоритмического решения с использованием популярных инструментальных средств [1, 7, 8].
Традиционные методы ML (деревья решений, линейные модели) часто более интерпретируемы [11], а НС, особенно глубокие, часто рассматриваются как «черные ящики», что может быть проблемой в критически важных программных решениях. При этом НС, как правило, требуют значительных вычислительных ресурсов и времени для обучения [4]. НС часто показывают высокую точность на сложных задачах (обработка изображений или естественного языка), но могут быть подвержены переобучению. Традиционные методы могут быть более экономичными [7, 8].
Сравнительный анализ способствует развитию новых методов и гибридных подходов, сочетающих преимущества различных алгоритмов [32].
В ходе разработки будет решаться задача прогнозирования временных рядов. В качестве датасета будут использоваться почасовые показания потребления электроэнергии с 2002 по 2018 г. Набор данных имеет два поля: дата («Datetime») и энергия в мегаваттах («PJME_MW»).
Целью работы является апробация алгоритмов, реализованных с помощью машинного и нейросетевого обучения, решения задачи прогнозирования временных рядов потребления электроэнергии.
В данной работе решаются следующие задачи:
1) Разработка алгоритмов прогнозирования с помощью XGBoost [5, 34].
2) Разработка алгоритмов прогнозирования с помощью Pytorch [27, 28].
3) Бенчмаркинг и оценка полученных результатов.
Результатами работы является бенчмаркинг [2, 16] и оценка метрик обученных моделей машинного и нейросетевого обучения, а также вычисление прогнозных значений потребления энергии с помощью «лучших» алгоритмов.
Основная часть
Постановка и анализ проблемы.
Вначале проведем анализ исходных данных, используя возможности библиотеки pandas [25], и визуализируем результаты с помощью графических инструментов [23, 30].
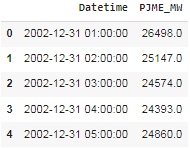
Для решения задачи прогнозирования загружаем исходный набор данных о потреблении энергии (рисунок 1).
import pandas as pd
df = pd.read_csv('PJME_hourly.csv')
df.head()
df.tail()
С помощью функции set_index устанавливаем индекс «Datetime» для первого столбца в загруженном наборе данных.
# Задание индекса в DateFrame в виде столбца Дата
df.set_index("Datetime", inplace=True)
df.head()
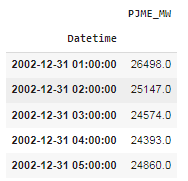
Набор данных о потреблении электроэнергии в мегаваттах представлен на рисунке 2.
|
Рисунок 1 – Исходный набор данных
Источник: составлено авторами |
Рисунок 2 – Набор данных с индексом
(«Datetime»)
Источник: составлено авторами |
import seaborn as sns
current_palette =sns.color_palette("deep")
sns.palplot(current_palette)
![]()
Рисунок 3 – Палитра seaborn («deep»)
Источник: составлено авторами
df.plot(title="PJME Energy use in MegaWatts",
figsize=(20, 8), style=".", color=sns.color_palette(current_palette) [4])
plt.xticks(rotation=45)
plt.show()
График потребления энергии в мегаваттах (МВт) представлен на рисунке 4.
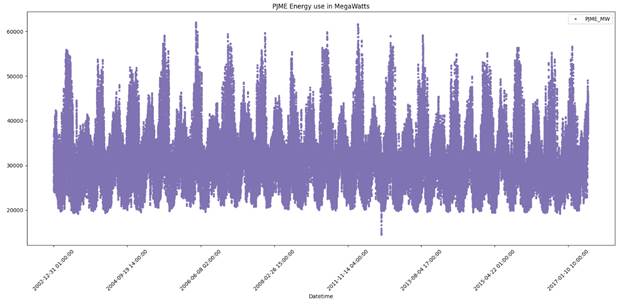
Рисунок 4 – График потребления энергии в мегаваттах (МВт)
Источник: составлено авторами
Для дальнейшей обработки значений индекса набора данных необходимо их преобразовать в объекты. Для этого используется функция to_datetime(df.index).
#Индекс относится к объектному типу, поэтому мы преобразуем его в datetime
df.index = pd.to_datetime(df.index)
Из рисунка 4 видно, что потребление энергии меняется в течение года.
Выдвинем гипотезу, что данные могут меняться в течение недели. Для оценки изменения такого потребления построим график.
train = df [df.index < "01-01-2015"]
test = df [df.index >= "01-01-2015"]
Для эксперимента построим свою палитру цветов для оформления графиков (рисунок 5).
color = ["green", "White", "Red", "Yellow", "Green", "Grey"]
sns.set_palette(color)
sns.palplot(sns.color_palette())
![]()
Рисунок 5 – Пользовательская палитра seaborn
Источник: составлено авторами
ax = df.loc [(df.index > '04-01-2018') & (df.index < '04-08-2018')] ['PJME_MW'] \
.plot(figsize=(15, 5), title='Потребление энергии за неделю', color=sns.color_palette(current_palette) [5])
plt.show()
График потребления энергии за неделю представлен на рисунке 6.
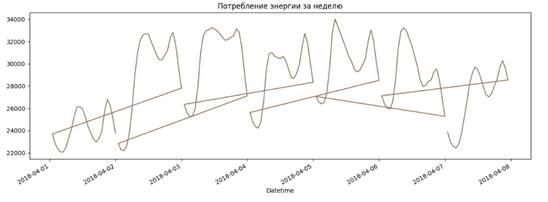
Рисунок 6 – График потребления энергии в течение недели
Источник: составлено авторами
Из рисунка 6 видно, что потребление энергии падает в ночное время. После чего заметен всплеск потребления в утренние часы. Потребление достигает своего максимума в вечернее время.
Далее создадим функцию create_features(df), которая создает копию DataFrame и добавляет новые столбцы: часы, дни недели, кварталы месяцы, годы, дни в году, дни в месяце, недели в году.
#для каждого дня в датасете есть возможность проведения анализа по разным критериям:
#- по дню недели Monday = 0 . . sunday = 6
#- по часам....
#что очень характерно для энергопотребления.
# Функция создания объектов временных рядов на основании индексов временных рядов
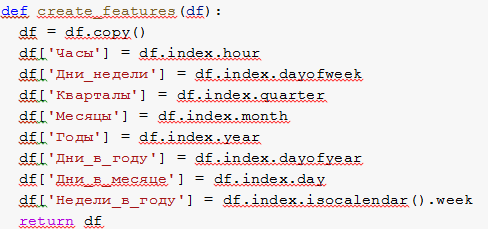
После создадим обновленный DataFrame, содержащий новые столбцы (рисунок 7).
# Создание DateFrame с дополнительными данными
df = create_features(df)
print(df)
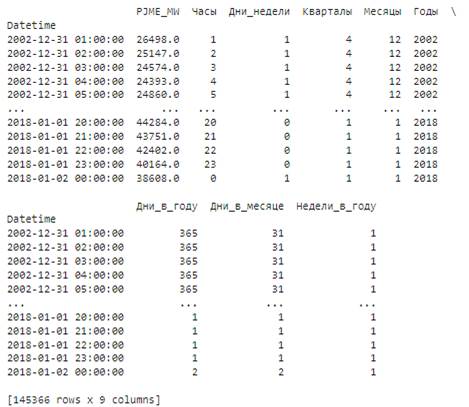
Рисунок 7 – Расширенный датасет
Источник: составлено авторами
Для дальнейшей оценки визуально представим потребление энергии по часам, месяцам и годам (рисунки 8-10), палитра «whitegrid».
# Визуальное представление данных потребления энергии по часам
plt.figure(figsize=(20,8))
sns.set_style('whitegrid')
sns.boxplot(x="Часы", y="PJME_MW", data=df, hue="Часы", palette="Blues")
plt.title("Распределение потребления электроэнергии по часам")
plt.show()
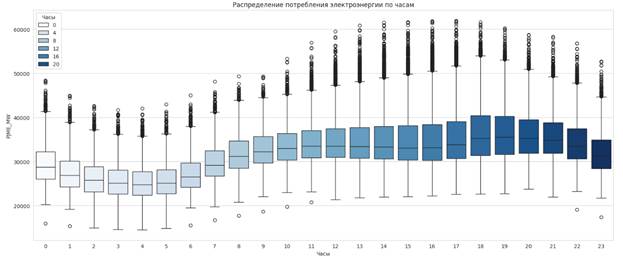
Рисунок 8 – График потребления энергии по часам
Источник: составлено авторами
# Визуальное представление данных потребления энергии по месяцам Самостоятельно
plt.figure(figsize=(20,8))
sns.boxplot(x="Месяцы", y="PJME_MW", data=df, hue="Месяцы")
plt.title("Распределение потребления электроэнергии по месяцам")
plt.show()
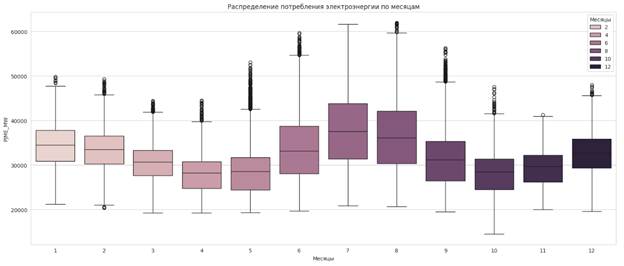
Рисунок 9 – График потребления энергии по месяцам
Источник: составлено авторами
Из рисунка 9 видно, что потребление энергии повышается в зимнее и летнее время, и уменьшается в весеннее и осеннее время. При этом максимум приходиться на июль, а минимум на апрель.
# Визуальное представление данных потребления энергии по годам
plt.figure(figsize=(20,8))
sns.set_style('darkgrid')
sns.boxplot(x="Годы", y="PJME_MW", data=df,hue="Годы", palette="BuGn")
plt.title("MW by year")
plt.show()
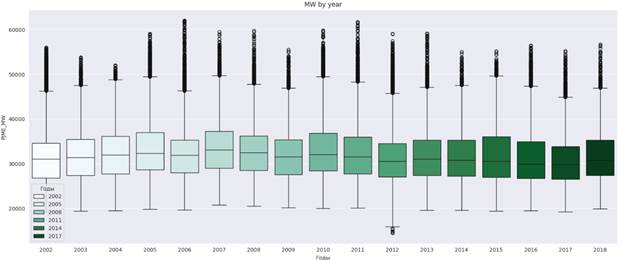
Рисунок 10 – График потребления энергии по годам
Источник: составлено авторами
На основании таких визуализаций авторами принято решение проводить эксперименты построения прогнозных моделей на основе данных первичного датасета (алгоритмы 1-ой группы) и расширенных, полученных алгоритмически (алгоритмы 2-ой группы).
В качестве экспериментов авторами были поставлены задачи сравнить методы машинного и нейросетевого обучения.
Методами машинного обучения выбраны алгоритмы градиентного бустинга деревьев решений, направленные на последовательное обучение ансамбля деревьев [14]. На каждой итерации вычисляются отклонения предсказаний обученного ансамбля на обучающей выборке. Новые деревья добавляются в ансамбль до тех пор, пока ошибка уменьшается, либо пока не выполняется одно из правил «ранней остановки».
Самым популярным таким алгоритмом на сегодня является XGBoost [9, 15]. Но растет интерес и к алгоритмам LightGBM и CatBoost [5, 6, 12, 13, 15, 17, 18, 19]. Приведем описание функциональных возможностей алгоритмов (таблица 1).
Таблица 1 – Характеристики алгоритмов градиентного бустинга
|
Алгоритм
|
Описание
|
Отличительные характеристики
|
|
XGBoost
(Extreme Gradient Boosting) |
оптимизированная и расширенная версия алгоритма
градиентного бустинга; разработана для повышения производительности и
скорости обучения
|
Скорость: оптимизирован для быстрого обучения
на больших наборах данных.
Регуляризация: L1 и L2. Параллелизация: поддерживает параллельные вычисления для ускорения обучения. Гибкость: поддерживает различные функции потерь и может использоваться для классификации, регрессии и ранжирования. |
|
LightGBM
(Light Gradient Boosting Machine)
|
реализация градиентного бустинга, разработанная
компанией Microsoft. Оптимизирована для работы с большими наборами данных и
высокой производительности.
|
Скорость: оптимизирован для быстрого обучения.
Эффективность памяти: использует алгоритмы, которые экономят память, такие как гистограммное дерево. Поддержка категориальных признаков: может эффективно работать с категориальными данными без необходимости предварительной обработки. Листовая параллелизация: поддерживает параллельное обучение на уровне листьев дерева. |
|
CatBoost (Categorical Boosting)
|
реализация градиентного бустинга, разработанная
компанией компанией Yandex. Оптимизирован для работы с категориальными
признаками.
|
Обработка категориальных признаков: автоматически
обрабатывает категории альные признаки, что упрощает подготовку данных.
Устойчивость к переобучению: использует методы, такие как рандомизация и бустинг. Простота использования: меньше требуется настройки гиперпараметров по сравнению с другими алгоритмами. Высокая точность: часто показывает высокую точность на задачах с категориальными данными. |
Для прогнозирования данных с использованием нейронных сетей авторами были выбраны рекуррентные сети (RNN), такие как LSTM (Long Short-Term Memory). Для экспериментов алгоритмы будут реализованы в PyTorch. Приведем описание отличительных особенностей фреймворка (таблица 2).
Таблица 2 – Характеристики PyTorch
|
Показатель
|
PyTorch
|
|
Архитектура
и дизайн
|
Разработан
Facebook AI Research (FAIR) как библиотека для глубокого обучения с акцентом
на гибкость и скорость разработки.
Использует динамические вычислительные графы, что делает его более интуитивно понятным для пользователей. Поддерживает распределенные вычисления и имеет интеграцию с другими инструментами, такими как TorchVision. |
|
Простота
использования и отладки
|
Благодаря
динамическим графам, PyTorch более интуитивен и прост в использовании,
особенно для тех, кто знаком с Python.
Проще в отладке, так как ошибки можно отслеживать в реальном времени. |
|
Производительность
и масштабируемость
|
Оптимизирован
для производительности и поддерживает распределенные вычисления.
Имеет хорошую поддержку GPU и интеграцию с библиотеками CUDA и cuDNN. |
|
Сообщество
и поддержка
|
Быстро
растущее сообщество, особенно в академических кругах и среди исследователей.
Хорошая документация и множество учебных материалов. |
|
Экосистема
и инструменты
|
Интеграция
с TorchVision, TorchText и TorchAudio для работы с изображениями, текстом и
аудио.
Поддержка ONNX для преобразования моделей в другие форматы. |
|
Развертывание
моделей
|
TorchServe
для развертывания моделей.
Поддержка ONNX для развертывания моделей на различных платформах. |
Описание решения.
Разработаем обобщенный алгоритм для всех последующих экспериментов:
- Загрузка данных: загружаем данные из файла PJME_hourly.csv. Предполагается, что последний столбец является целевым.
- Разделение данных: данные разделяются на обучающую и тестовую выборки в соотношении 80/20.
- Обучение моделей: обучаем модели на обучающей выборке.
- Оценка моделей: предсказываем значения для тренировочной и тестовой выборок и вычисляем среднеквадратичную ошибку (MSE) для каждой модели.
- Вывод результатов: выводим MSE для каждой модели.
Алгоритмы 1-ой группы.
Далее приведены алгоритмы построения прогнозных моделей на основе данных первичного датасета потребления энергии.
Алгоритм градиентного бустинга на основе XGBoost (1.1).
Подключение основных зависимостей в проект [29].
![]()
Загрузка данных из файла-источника с форматом csv.
df = pd.read_csv('PJME_hourly.csv')
Преобразование столбцов исходного датасета («Datetime») и формирование входящих переменных для модели ML (x, y).
df ['Datetime'] = pd.to_datetime(df ['Datetime'])
# Преобразование datetime в UNIX timestamp (число с плавающей запятой)
df ['Datetime'] = df ['Datetime'].astype('int64') // 10**9 #Преобразование в секунды
# целевая переменная называется 'PJME_MW'
x = df.drop('PJME_MW', axis=1)
y = df ['PJME_MW']
Следующим шагом необходимо разделить набор данных на обучающий и тестовый.
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
Создадим XGBRegressor [9]. Установим параметры обучения модели ML, в том числе ошибку MSE (squarederror).
import xgboost as xgb
# Создание регрессора xgboost
reg = xgb.XGBRegressor(base_score=0.5, booster='gbtree',
n_estimators=1200,
early_stopping_rounds=50,
objective='reg:squarederror',
max_depth=3,
learning_rate=0.01)
Примечание: XGBRegressor - это часть библиотеки xgboost, которая интегрируется с scikit-learn. Удобный интерфейс для пользователей, знакомых с scikit-learn. Возможно, для формирования регрессора потребуется версия scikit-learn==1.3.1: pip install scikit-learn==1.3.1)
Чтобы замерить время выполнения обучения алгоритмов авторами применялись возможности библиотеки time. Далее по тексту будут ссылки на этот код:
import time
print('Lets GO!')
start = time.time()
s=time.ctime(start)
# **********обучение************
end = time.time()
e=time.ctime(end)
print('all done!')
print('started', s)
print('finished', e)
print('sec', end-start)
С помощью метода fit(x_train, y_train, eval_set= [(x_train, y_train), (x_test, y_test)], verbose=100) происходит обучение первой модели на всем наборе данных. В качестве параметров передаем в метод обучающий набор данных, eval_set – набор для проверки (направлен на отслеживание производительность модели) и verbose – количество итераций, на которых выводится проверка.

Значение среднеквадратичной ошибки уменьшается по ходу обучения модели как на тренировочном наборе данных, так и на тестовом.
На следующем шаге с помощью функции predict(x_test) делаем прогноз для тестового набора данных.
# Прогноз для тестового набора данных
predict=reg.predict(x_test)
x_test ['Прогноз'] = predict
import numpy as np
from sklearn.metrics import mean_squared_error
# Вычисление среднеквадратичной ошибки на тестовом наборе
score = np.sqrt(mean_squared_error(y_test, predict))
print('Значение среднеквадратичной ошибки на тестовом наборе:')
print(score)
![]()
Далее представим полученные данные в виде графика, на котором будут реальные данные потребления энергии и прогнозируемые (рисунок 12). Для этого создадим клон датасета: переменная copy.
copy = pd.read_csv('PJME_hourly.csv')
И с помощью следующего метода добавим столбец-прогноз к набору данных (рисунок 11).
# Добавление столбца прогноз к набору данных
copy = copy.merge(x_test [ ['Прогноз']], how='left', left_index=True, right_index=True)
copy.head()
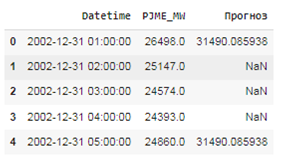
Рисунок 11 – Вывод значений датафрейма-копии
с новым столбцом «Прогноз»
Источник: составлено авторами

ax = copy [ ['PJME_MW']].plot(figsize=(15, 5))
copy ['Прогноз'].plot(ax=ax, style='.')
plt.legend( ['Реальные данные', 'Прогноз'])
ax.set_title('Реальные данные потребления и прогноз')
plt.show()
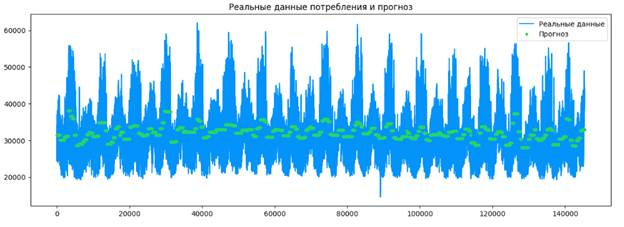
Рисунок 12 – Вывод графика потребления энергии с реальными и прогнозными значениями
Источник: составлено авторами
Вначале на основе анализа данных были получены зависимости потребления энергии в течение недели. Проверим эту гипотезу и выведем соответствующий график, предварительно сделав срез (loc) на индексированный столбец («Datetime») датасета-копии на одну неделю (рисунок 13).
# Задание индекса в DateFrame в виде столбца Дата
copy.set_index("Datetime", inplace=True)
#Индекс относится к объектному типу, поэтому мы преобразуем его в datetime
copy.index = pd.to_datetime(copy.index)
# Визуальное представление реальных данных и прогноза за неделю
ax = copy.loc [(copy.index > '04-01-2018') & (copy.index < '04-08-2018')] ['PJME_MW'] \
.plot(figsize=(15, 5), title='Потребление энергии за неделю')
copy.loc [(copy.index > '04-01-2018') & (copy.index < '04-08-2018')] ['Прогноз'].plot(style='.')
plt.legend( ['Реальные данные', 'Прогноз'])
plt.show()
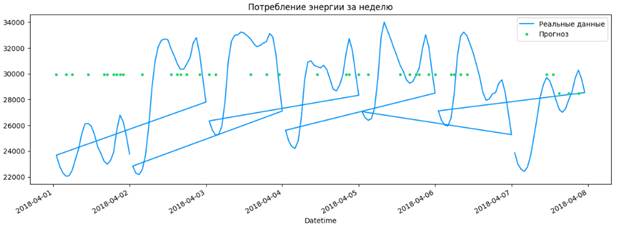
Рисунок 13 – Вывод графика потребления энергии с реальными и прогнозными значениями
Источник: составлено авторами
Примечание: возможно, выборку нужно будет подбирать самостоятельно в разных экспериментах, так как разделение данных на тренировочные и тестовые происходит случайным образом.
Алгоритмы градиентного бустинга на основе LightGBM и CatBoost (1.2, 1.3).
Алгоритм предполагает следующие шаги, код которых описан в первом алгоритме: загрузка данных; преобразование столбца даты в datetime (без создания индекса!); преобразование datetime в UNIX timestamp (число с плавающей запятой); формирование входящих переменных для модели ML (x, y), целевая переменная в датасете называется «PJME_MW»; разделение данных на обучающую и тестовую выборки.
Установим базовые зависимости для библиотек бустинга.
pip install catboost
import lightgbm as lgb
from catboost import CatBoostRegressor
Примечание: Возможно, потребуется установка дополнительной библиотеки dask для корректной работы бустинга (библиотека для параллельных вычислений в Python): pip install dask.
Используя LGBMRegressor и CatBoostRegressor, создадим новые модели ML, проведем их обучение и прогнозирование, выведем значение ошибок обучения.
# LightGBM
lgb_model = lgb.LGBMRegressor(learning_rate=0.01,force_row_wise="true")
lgb_model.fit(x_train, y_train)
y_pred_lgb = lgb_model.predict(x_test)
mse_lgb = mean_squared_error(y_test, y_pred_lgb)

# CatBoost
catboost_model = CatBoostRegressor(verbose=0)
catboost_model.fit(x_train, y_train, verbose=100)
y_pred_catboost = catboost_model.predict(x_test)
mse_catboost = mean_squared_error(y_test, y_pred_catboost)
![]()
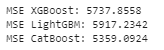
# Вывод результатов
print(f"MSE XGBoost: {score:.4f}")
print(f"MSE LightGBM: {np.sqrt(mse_lgb):.4f}")
print(f"MSE CatBoost: {np.sqrt(mse_catboost):.4f}")
Алгоритм рекуррентной нейронной сети в PyTorch (1.4).
import pandas as pd
Загрузка данных о потреблении энергии.
# data =pd.read_csv('PJME_hourly.csv')
Подключение базовых зависимостей.
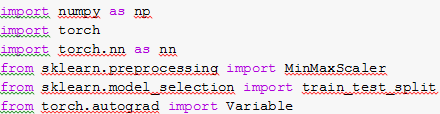
Создание индекса на столбец «Datetime».
data ['Datetime'] = pd.to_datetime(data ['Datetime'])
data.set_index('Datetime', inplace=True)
Далее необходимо провести нормализацию данных в наборе. Для этого используем функцию MinMaxScaler(feature_range=(0, 1)), которая преобразует все значения согласно заданному интервалу. Так в качестве -1 будет принято самое минимальное значение, а в качестве 1 будет принято наибольшее. С помощью метода fit_transform(data.values) вычисляются статистические показатели, и после этого происходит масштабирование данных.
scaled_data = scaler.fit_transform(data.values)
Создадим функцию create_dataset(dataset, time_step), которая будет подготавливать DataFrame для решения задачи прогнозирования. В качестве параметров функция принимает исходный набор данных и переменную, которая будет хранить «количество шагов назад» (в эксперименте 100 дней назад), на основании которых будет делаться прогноз.
# Подготовка данных для LSTM
def create_dataset(dataset, time_step=1):
dataX, dataY = [], []
for i in range(len(dataset) - time_step - 1):
a = dataset [i:(i + time_step), 0]
dataX.append(a)
dataY.append(dataset [i + time_step, 0])
return np.array(dataX), np.array(dataY)
Создадим новый набор данных, который содержит столбцы исходного набора данных и столбцы со значениями, на основании которых будет строиться прогноз. В X (набор данных) поместим все столбцы, на основании которых будет делаться прогноз. В у (набор меток) поместим столбец со значениями потребления энергия, для которых будет делаться прогноз.
time_step = 100
X, y = create_dataset(scaled_data, time_step)
Затем разделим набор данных.
# Разделение данных на обучающую и тестовую выборки
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Выполним преобразование переменных.
# Преобразование данных
X_train = X_train.reshape(X_train.shape [0], X_train.shape [1], 1)
X_test = X_test.reshape(X_test.shape [0], X_test.shape [1], 1)
# Преобразование в тензоры torch
X_train = torch.from_numpy(X_train).float()
y_train = torch.from_numpy(y_train).float()
X_test = torch.from_numpy(X_test).float()
y_test = torch.from_numpy(y_test).float()
Разработаем класс LSTMModel для разработки рекуррентной модели НС [33]. В классе создадим конструктор (__init__), который будет принимать следующие аргументы:
- input_size – количество объектов, которые подаются в модель на каждой итерации;
- hidden_layer_size – число нейронов в скрытом слое;
- output_size – количество слоев в выходном слое модели.
В конструкторе __init__ создадим слой lstm и выходной слой linear. В методе forward(self, input_seq) происходит описание способа, по которому данные перемещаются по модели.
# Определение модели LSTM
class LSTMModel(nn.Module):
def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
super(LSTMModel, self).__init__()
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size),
torch.zeros(1, 1, self.hidden_layer_size))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), -1, 1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions [-1]
Создадим модель, инициализируем функцию потерь и оптимизатор.
# Инициализация модели, функции потерь и оптимизатора
model = LSTMModel()
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
Структура LSTM модели представлена на рисунке 14. Структура имеет два слоя, первый состоит из ста нейронов.

Рисунок 14 – Структура LSTM модели
Источник: составлено авторами
Произведем обучение модели. Данный алгоритм потребует расчета времени выполнения, для этого воспользуемся приведенным выше кодом на основе библиотеки time.
# код time
epochs = 1
for i in range(epochs):
for seq, labels in zip(X_train, y_train):
optimizer.zero_grad()
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
y_pred = model(seq)
single_loss = loss_function(y_pred, labels)
single_loss.backward()
optimizer.step()
# код time
print(f'Epoch {i} loss: {single_loss.item()}')
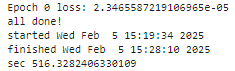
Выполним прогнозирование данных на тренировочной и тестовой выборках.
model.eval()
train_predict = []
test_predict = []
for seq in X_train:
with torch.no_grad():
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
train_predict.append(model(seq).item())
for seq in X_test:
with torch.no_grad():
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
test_predict.append(model(seq).item())
Далее потребуется обратное преобразование данных [24].
train_predict = scaler.inverse_transform(np.array(train_predict).reshape(-1, 1))
test_predict = scaler.inverse_transform(np.array(test_predict).reshape(-1, 1))
y_train = scaler.inverse_transform(y_train.detach().numpy().reshape(-1, 1))
y_test = scaler.inverse_transform(y_test.detach().numpy().reshape(-1, 1))
Вывод метрик моделирования и визуализация реальных и прогнозных значений части данных (произведена выборка) датасета (рисунок 15).
# Оценка модели
import math
from sklearn.metrics import mean_squared_error
train_rmse = math.sqrt(mean_squared_error(y_train, train_predict))
test_rmse = math.sqrt(mean_squared_error(y_test, test_predict))
print(f"Train RMSE: {train_rmse:.4f}")
print(f"Test RMSE: {test_rmse:.4f}")
![]()
import matplotlib.pyplot as plt
# Выбор части данных (например, первые 50 точек тестовой выборки)
subset_indices = range(50)
y_test_subset = y_test [subset_indices]
y_pred_subset = test_predict [subset_indices]
# Визуализация результатов
plt.figure(figsize=(12, 6))
plt.plot(y_test_subset, label='Real data', color='blue')
plt.plot(y_pred_subset, label='Predictions', color='red')
plt.title('Real vs Predicted values (Subset)')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()
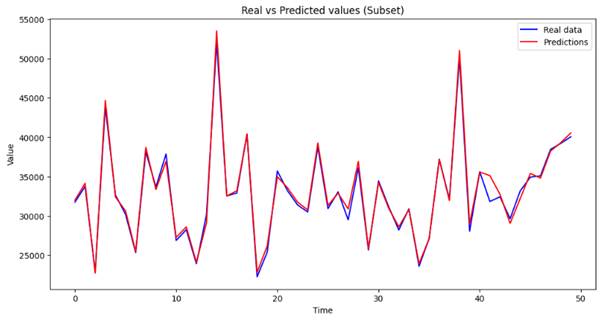
Рисунок 15 – Вывод графика потребления энергии с реальными и прогнозными значениями
Источник: составлено авторами
Алгоритмы 2-ой группы
Далее приведены алгоритмы построения прогнозных моделей на основе расширенных данных датасета потребления электроэнергии.
Алгоритм градиентного бустинга на основе XGBoost (2.1).
Подключение основных зависимостей в проект, загрузка данных, преобразование столбца с датами в формат datetime:

# Загрузка данных
file_path = 'PJME_hourly.csv'
data = pd.read_csv(file_path)
# Преобразование столбца с датами в формат datetime
data ['Datetime'] = pd.to_datetime(data ['Datetime'])
Создание дополнительных признаков распределения потребления энергии.
data ['Часы'] = data ['Datetime'].dt.hour
data ['Дни_недели'] = data ['Datetime'].dt.dayofweek
data ['Кварталы'] = data ['Datetime'].dt.quarter
data ['Месяцы'] = data ['Datetime'].dt.month
data ['Годы'] = data ['Datetime'].dt.year
data ['Дни_в_году'] = data ['Datetime'].dt.dayofyear
data ['Дни_в_месяце'] = data ['Datetime'].dt.day
data ['Недели_в_году'] = data ['Datetime'].dt.isocalendar().week
Формирование переменных модели ML (x, y), нормализация.
# Предполагаем, что последний столбец - целевой
X = data.drop(columns= ['Datetime', 'PJME_MW']).values
y = data ['PJME_MW'].values
# Нормализация данных
scaler = MinMaxScaler(feature_range=(0, 1))
X_scaled = scaler.fit_transform(X)
y_scaled = scaler.fit_transform(y.reshape(-1, 1)).ravel()
Разделение данных на обучающую и тестовую выборки с сохранением первоначальных индексов (indices_train, indices_test), что позволит в дальнейшем для прогнозных значений найти первоначальные (сопоставить с реальными из датасета и построить корректно графики).
X_train, X_test, y_train, y_test, indices_train, indices_test = train_test_split(
X_scaled, y_scaled, range(X_scaled.shape [0]), test_size=0.2, random_state=42)
Создание модели XGBRegressor.
# Создание модели XGBRegressor
model = xgb.XGBRegressor(base_score=0.5, booster='gbtree',
n_estimators=1000,
early_stopping_rounds=50,
objective='reg:squarederror',
max_depth=3,
learning_rate=0.01)
Обучение модели XGBRegressor с учетом времени выполнения.
# Обучение модели с отслеживанием потерь
eval_set = [(X_train, y_train), (X_test, y_test)]
# код time
bst=model.fit(X_train, y_train, eval_set=eval_set, verbose=True)
# код time

Получение результатов оценки: метрика MSE (squarederror).
# Получение результатов оценки
results = model.evals_result()
epochs = len(results ['validation_0'] ['rmse'])
x_axis = range(0, epochs)
Проведение прогнозирования на тренировочной и тестовой выборках.
# Прогнозирование
y_pred_train = bst.predict(X_train)
y_pred_test = bst.predict(X_test)
Вывод метрики оценки качества модели.
# Оценка модели
len_train=len(results ['validation_0'] ['rmse'])
len_test=len(results ['validation_1'] ['rmse'])
print(f"Train RMSE: { results ['validation_0'] ['rmse'] [len_train-1]:.4f}")
print(f"Test RMSE: { results ['validation_1'] ['rmse'] [len_test-1]:.4f}")
![]()
Алгоритмы градиентного бустинга на основе LightGBM и CatBoost (2.2, 2.3).
Код по загрузке и преобразованию данных опущен, так как идентичен коду алгоритма первого раздела.
Используя LGBMRegressor и CatBoostRegressor [3], создадим новые модели ML, проведем их обучение и прогнозирование, выведем значение ошибок обучения.
# LightGBM
lgb_model = lgb.LGBMRegressor(objective='regression', metric='rmse', n_estimators=1000, learning_rate=0.01,force_col_wise="true", verbose=100)
lgb_model.fit(X_train, y_train)
y_pred_lgb = lgb_model.predict(X_test)
mse_lgb = mean_squared_error(y_test, y_pred_lgb)
![]()
# CatBoost
catboost_model = CatBoostRegressor(iterations=1000, learning_rate=0.1, depth=6, loss_function='RMSE', verbose=100)
catboost_model.fit(X_train, y_train)
y_pred_catboost = catboost_model.predict(X_test)
mse_catboost = mean_squared_error(y_test, y_pred_catboost)
![]()
import numpy as np
print(f"MSE LightGBM: { np.sqrt(mse_lgb):.4f}")
print(f"MSE CatBoost: { np.sqrt(mse_catboost):.4f}")
![]()
Алгоритмы градиентного бустинга на основе xgb.train (2.4).
Так как алгоритмы второй группы показали лучше результаты, чем первой, было принято решение именно для расширенного датасета провести эксперимент на моделирование бустинга на низком уровне, используя xgb.train [26, 35], для сравнения с результатами, полученными на основе XGBRegressor.
XGBRegressor и xgb.train - это два разных способа использования библиотеки XGBoost для обучения моделей градиентного бустинга. Они предназначены для разных целей и имеют разные особенности.
Интерфейс XGBRegressor - это часть библиотеки xgboost, которая интегрируется с scikit-learn. Используется для задач регрессии. Он предоставляет стандартный интерфейс scikit-learn, такой, как методы fit(), predict(), score() и т.д. Параметры модели задаются через конструктор класса и их можно настраивать.
Интерфейс xgb.train - это более низкоуровневый интерфейс, предоставляемый библиотекой xgboost. Он позволяет более гибко управлять процессом обучения и предоставляет доступ к дополнительным функциям. Используется для обучения моделей как для регрессии, так и для классификации. Позволяет более детально настраивать процесс обучения, включая использование пользовательских функций потерь и метрик оценки. Параметры модели задаются в виде словаря и передаются в функцию xgb.train.
Установим базовые зависимости для алгоритма.
Этапы загрузки данных, преобразования столбца с датами в формат datetime, создание дополнительных признаков, формирование переменных модели, их нормализация, а также разделение данных на обучающую и тестовую выборки с сохранением индексов (indices_train, indices_test) остаются прежними (как в 2.1).
Создадим дополнительную переменную, используя DMatrix для XGBoost.
# Создание DMatrix для XGBoost
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)
Установим параметры модели.
# Параметры модели
params = {
'objective': 'reg:squarederror',
'tree_method': 'hist',
'eval_metric': 'rmse'
}
Проведем обучение модели с учетом времени выполнения кода.
# Обучение модели с отслеживанием потерь
# код time
evals = [(dtrain, 'train'), (dtest, 'test')]
evals_result = {}
bst = xgb.train(
params=params,
dtrain=dtrain,
evals=evals,
evals_result=evals_result,
num_boost_round=100,
verbose_eval=True
)
# код time
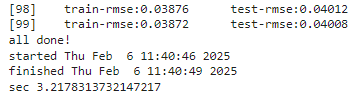
Построим прогноз и выведем метрики оценки качества модели.
# Прогнозирование
y_pred_train = bst.predict(dtrain)
y_pred_test = bst.predict(dtest)
# Оценка модели
len_train=len(evals_result ['train'] ['rmse'])
len_test=len(evals_result ['test'] ['rmse'])
print(f"Train RMSE: {evals_result ['train'] ['rmse'] [len_train-1]:.4f}")
print(f"Test RMSE: {evals_result ['test'] ['rmse'] [len_test-1]:.4f}")
![]()
Алгоритм рекуррентной нейронной сети в PyTorch (2.5).
Подключение базовых зависимостей.
import torch
import torch.nn as nn
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
Загрузка данных, преобразование столбца с датами в формат datetime (без индекса!) останутся прежними (как в 1.4).
Создание дополнительных признаков распределения потребления энергии аналогично такому же пункту алгоритма 2.1.
Произведем формирование переменных модели НС.
X = data.drop(columns= ['Datetime', 'PJME_MW']).values
y = data ['PJME_MW'].values
Нормализация данных.
scaler = MinMaxScaler(feature_range=(0, 1))
X_scaled = scaler.fit_transform(X)
y_scaled = scaler.fit_transform(y.reshape(-1, 1))
При разделении данных на обучающую и тестовую выборки сохраним индексы тестового набора.
X_train, X_test, y_train, y_test, indices_train, indices_test = train_test_split(X_scaled, y_scaled, range(X_scaled.shape [0]), test_size=0.2, random_state=42)
Преобразование данных в тензоры.
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)
Добавим класс LSTMModel [21, 22], создадим модель, инициализируем функцию потерь и оптимизатор аналогично алгоритму 1.4.
Произведем обучение модели также аналогично алгоритму рекуррентной сети первой группы.
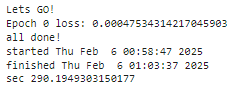
Выполним прогнозирование данных на тренировочной и тестовой выборках (код аналогичен в 1.4).
Выведем метрики моделирования.
# Оценка модели
import math
from sklearn.metrics import mean_squared_error
train_rmse = math.sqrt(mean_squared_error(y_train, train_predict))
test_rmse = math.sqrt(mean_squared_error(y_test, test_predict))
print(f"Train RMSE: {train_rmse:.4f}")
print(f"Test RMSE: {test_rmse:.4f}")
![]()
Алгоритм SimpleLinearModel в PyTorch (2.6).
Результаты моделирования в PyTorch показали весьма хорошие метрики. Авторами поставлена задача модифицировать алгоритм НС и реализовать задачу на основе алгоритма ML – линейной регрессии [20, 31].
Для этого был разработан класс SimpleLinearModel, отвечающий за модель на основе линейной регрессии.
# Определение модели
class SimpleLinearModel(nn.Module):
def __init__(self, input_dim):
super(SimpleLinearModel, self).__init__()
self.linear = nn.Linear(input_dim, 1)
def forward(self, x):
return self.linear(x)
Создание и обучение модели.
# Создание модели
input_dim = X_train.shape [1]
model1 = SimpleLinearModel(input_dim)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# Обучение модели
# код time
num_epochs = 100
for epoch in range(num_epochs):
model1.train()
optimizer.zero_grad()
outputs = model1(X_train)
loss = criterion(outputs, y_train)
loss.backward()
optimizer.step()
# код time
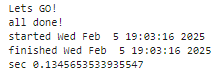
Оценка модели (код аналогичен другим алгоритмам).
![]()
Оценка и анализ прогнозирования
Для анализа результатов проведенных экспериментов, сформируем сводную таблицу, содержащую наименование алгоритма, метрики быстродействия и ошибки обучения по тестовой выборке (таблица 3).
Таблица 3 – Результаты работы авторских алгоритмов
|
Название алгоритма ML/НС
|
Время
обучения модели, сек
|
Значение среднеквадратичной ошибки (Test RMSE)
|
|
Алгоритмы
1-ой группы
| ||
|
XGBRegressor
(1.1)
|
12
|
5737,8558
|
|
LightGBM (1.2)
|
10,2
|
5917,2342
|
|
CatBoost (1.3)
|
14,9
|
5359,0924
|
|
LSTM
в PyTorch (1.4)
|
516,3282
|
769,7354
|
|
Алгоритмы
2-ой группы
| ||
|
XGBRegressor
(2.1)
|
23,5563
|
0,0668
|
|
LightGBM (2.2)
|
21,5
|
0,0532
|
|
CatBoost (2.3)
|
22,7
|
0,0430
|
|
xgb.train (2.4)
|
3,21
|
0,0401
|
|
LSTM
в PyTorch (2.5)
|
582,1132
|
0,0746
|
|
SimpleLinearModel в PyTorch (2.6)
|
0,13
|
0,29
|
Результаты прогнозирования с помощью увеличенного (расширенного авторами алгоритмически) датасета существенно отличаются от экспериментов первой группы.
Алгоритмы первой группы «выигрывают» лишь в скорости обучения моделей.
Стоит отметить, что алгоритмы ML (бустинг) первой группы экспериментов значительно уступают метрикам качества нейросетевого моделирования с помощью рекуррентной модели.
По скорости обучения бустинг всегда находил решение быстрее, чем модели на основе НС.
Значения среднеквадратичной ошибки согласно результатам алгоритмов второй группы отклоняются друг от друга незначительно, что позволяет сделать вывод о необходимости проведения детального преданализа данных текущего датасета.
Впечатлила скорость обучения алгоритма из второй группы, использующего линейную регрессию (2.6) в библиотеке PyTorch. Несмотря на повышенное незначительно значение метрики качества, такой алгоритм ML можно рекомендовать для текущей задачи, особенно если вычисление происходит на низко производительных машинах.
Лучшим алгоритмом в данной «битве» является алгоритм ML на основе низкоуровневого бустинга xgb.train. Именно для него выведем графические результаты прогнозного моделирования потребления электроэнергии. Для доказательства возможности использования результатов алгоритма построим график (рисунок 16) наблюдения расхождения (согласования) метрик качества на основе тренировочных и тестовых данных (эффект переобучения).
# График потерь

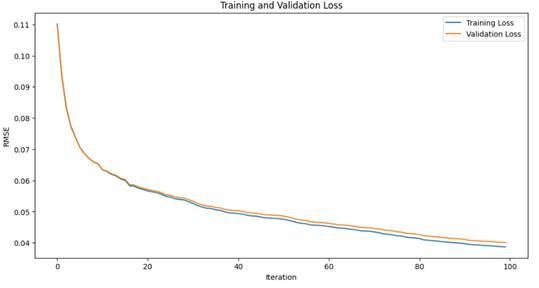
Рисунок 16 – Вывод графика ошибок
Источник: составлено авторами
Как видно из графика, переобучения нет.
Преобразуем прогнозные данные, полученные алгоритмически, обратное кодирование.
# Обратное преобразование данных
y_test_actual = scaler.inverse_transform(y_test.reshape(-1, 1)).ravel()
y_pred_train_actual = scaler.inverse_transform(y_pred_train.reshape(-1, 1)).ravel()
y_pred_test_actual = scaler.inverse_transform(y_pred_test.reshape(-1, 1)).ravel()
Выберем строки из исходного DataFrame, соответствующие тестовому набору.
data_test = data.iloc [indices_test].reset_index(drop=True)
data_test ['Predicted'] = y_pred_test_actual
Приведем визуализацию результатов прогнозирования относительно различных временных разрезов (рисунки 17-24), код организуем в цикле по всем выборкам переменной time_features.
time_features = ['Часы', 'Дни_недели', 'Кварталы', 'Месяцы', 'Годы', 'Дни_в_году', 'Дни_в_месяце', 'Недели_в_году']
for feature in time_features:
plt.figure(figsize=(12, 6))
plt.plot(data_test.groupby(feature) ['PJME_MW'].mean(), label='Real data', color='blue')
plt.plot(data_test.groupby(feature) ['Predicted'].mean(), label='Predictions', color='red')
plt.title(f'Real vs Predicted values by {feature}')
plt.xlabel(feature)
plt.ylabel('Value')
plt.legend()
plt.show()


|
Рисунок 17 – Вывод графика
потребления энергии по часам
Источник: составлено авторами |
Рисунок 18 – Вывод графика
потребления энергии по дням недели
Источник: составлено авторами |


|
Рисунок 19 – Вывод графика
потребления энергии по кварталам
Источник: составлено авторами |
Рисунок 20 – Вывод графика
потребления энергии по месяцам
Источник: составлено авторами |


|
Рисунок 21 – Вывод графика
потребления энергии по годам
Источник: составлено авторами |
Рисунок 22 – Вывод графика
потребления энергии дням в году
Источник: составлено авторами |

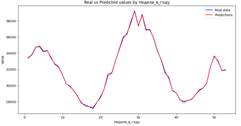
|
Рисунок 23 – Вывод графика
потребления энергии по дням в месяце
Источник: составлено авторами |
Рисунок 24 – Вывод графика
потребления энергии по неделям в году
Источник: составлено авторами |
Авторами разработаны алгоритмы прогнозирования с применением библиотек pandas, numpy, matplotlib, seaborn, xgboost, lightgbm, catboost, scikit-learn, pytorch, time.
В ходе анализа и оценки полученных результатов была выявлена высокая точность прогноза на основе методов и ML и НС. Среди недостатков можно выделить долгий процесс обучения алгоритмов (модели), построенных на основе рекуррентной НС в Pytorch. Но считать это недостатком весьма некорректно, так как эксперименты проводились на CPU. Для решения этой проблемы необходимо использовать центральный процессор с большей производительностью или применять GPU. Но, тем не менее, все алгоритмы ML оказались более производительными, и обошли НС по скорости обучения моделей.
Рассматриваемые библиотеки градиентного бустинга XGBoost оптимизированы для высокой производительности, но LightGBM и XGBoost в некоторых экспериментах оказались быстрее.
Интерфейс XGBRegressor с высокоуровневым интерфейсом интегрируемый с scikit-learn «уступил» в качестве обучения модели низкоуровневому xgb.train.
Можно выделить эффективность НС по сравнению с классическими способами решения практических задач в алгоритмах первой группы (на исходном датасете).
Лучшим алгоритмом в данной «битве» является алгоритм ML на основе низкоуровневого бустинга xgb.train.
Выбор между XGBoost, xgb.train и LSTM в PyTorch зависит от целей исследования и условий проведения экспериментов (вычислительные мощности):
- бустинг может быть предпочтительным для исследователей и тех, кто предпочитает гибкость и простоту в использовании.
- LSTM может быть лучшим выбором для приложений, где требуется масштабируемость, распараллеливание и поддержка большого количества инструментария и библиотек.
Решения и на основе ML и на НС активно развиваются, и выбор между ними может также зависеть от личных предпочтений и опыта.
Источники:
2. Бенчмаркинг: пошаговая схема работы. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/articles/718786/ (дата обращения: 10.02.2025).
3. Градиентный бустинг. Реализация с нуля на Python и разбор особенностей его модификаций (XGBoost, CatBoost, LightGBM). Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/articles/799725/ (дата обращения: 09.02.2025).
4. Багно А.С., Жилина Е.В. Как искусственный интеллект меняет учебные методики и ученический опыт. / Научный вектор: Сборник научных трудов. - Ростов-на-Дону : Ростовский государственный экономический университет «РИНХ», 2024. – 307-309 c.
5. Как работает нативная поддержка категорий в XGBoost. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/companies/skillfactory/articles/724722/ (дата обращения: 08.02.2025).
6. Как разработать ансамбль Light Gradient Boosted Machine (LightGBM). Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/companies/ (дата обращения: 09.02.2025).
7. Жуков А.В., Жилина Е.В. Модели и алгоритмы генерации синтетических наборов данных для ML // Информатизация в цифровой экономике. – 2021. – № 3. – c. 95-102. – doi: 10.18334/ide.2.3.113388.
8. Жилина Е.В., Ефимова Е.В., Рутта Н.А., Савская А.Р. Нейро-нечеткий подход к прогнозированию рисков информационной безопасности в вузе // Интеллектуальные ресурсы - региональному развитию. – 2020. – № 2. – c. 132-137.
9. Особенности валидации моделей на Xgboost. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/articles/573040/ (дата обращения: 10.02.2025).
10. Скляров А.В., Тищенко Е.Н., Ефимова Е.В., Жилина Е.В. Оценка эффективности мероприятий информационной безопасности на защищенных экономических системах с применением искусственных нейронных сетей // Экономические науки. – 2019. – № 177. – c. 77-81. – doi: 10.14451/1.177.77.
11. Никифоренко Д.А., Карапетян А.А., Ефимова Е.В. Применение машинного обучения и искусственного интеллекта в анализе данных и цифровизации бизнес-процессов // Новые направления научной мысли: Сборник научных статей Национальной (Всероссийской) научно-практической конференции. Ростов-на-Дону, 2023. – c. 502-505.
12. Разбираем особенности алгоритмов CatBoost и LightGBM: какой от них профит. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/companies/tochka/articles/751012/ (дата обращения: 09.02.2025).
13. Разбираем особенности алгоритмов CatBoost и LightGBM: какой от них профит. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/companies/tochka/articles/751012/ (дата обращения: 08.02.2025).
14. Верютина В.В., Дзюба А.Г., Жилина Е.В. Сегментация клиентской базы методом k-средних // Проблемы проектирования, применения и безопасности информационных систем в условиях цифровой экономики: Материалы XXII Международной научно-практической конференции. Ростов-на-Дону, 2022. – c. 50-55.
15. Три подхода к ускорению обучения XGBoost-моделей. Habr.com. [Электронный ресурс]. URL: https://habr.com/ru/companies/wunderfund/articles/665278/ (дата обращения: 10.02.2025).
16. Что такое бенчмаркинг. Timeweb.com. [Электронный ресурс]. URL: https://timeweb.com/ru/community/articles/chto-takoe-benchmarking (дата обращения: 08.02.2025).
17. LightGBM Classifier in Python. Kaggle.com. [Электронный ресурс]. URL: http://kaggle.com/code/prashant111/lightgbm-classifier-in-python (дата обращения: 09.02.2025).
18. LightGBM в машинном обучении. Datafinder.ru. [Электронный ресурс]. URL: https://datafinder.ru/products/lightgbm-v-mashinnom-obuchenii (дата обращения: 09.02.2025).
19. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Proceedings.neurips.cc. [Электронный ресурс]. URL: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (дата обращения: 10.02.2025).
20. Linear Regression. Datatab.net. [Электронный ресурс]. URL: https://datatab.net/tutorial/linear-regression (дата обращения: 10.02.2025).
21. Long Short Term Memory (LSTM) Networks using PyTorch. Geeksforgeeks.org. [Электронный ресурс]. URL: https://www.geeksforgeeks.org/long-short-term-memory-networks-using-pytorch/ (дата обращения: 08.02.2025).
22. LSTM for Time Series Prediction in PyTorch. Machinelearningmastery.com. [Электронный ресурс]. URL: https://machinelearningmastery.com/lstm-for-time-series-prediction-in-pytorch/ (дата обращения: 08.02.2025).
23. Matplotlib. [Электронный ресурс]. URL: https://matplotlib.org/ (дата обращения: 07.02.2025).
24. NumPy. [Электронный ресурс]. URL: https://numpy.org/ (дата обращения: 06.02.2025).
25. Pandas. [Электронный ресурс]. URL: https://pandas.pydata.org/ (дата обращения: 06.02.2025).
26. Parameterize XGBoost with xgboost.train for regression. Kaggle.com. [Электронный ресурс]. URL: https://www.kaggle.com/discussions/general/197091 (дата обращения: 09.02.2025).
27. PyTorch. Wikipedia.org. [Электронный ресурс]. URL: https://ru.wikipedia.org/wiki/PyTorch (дата обращения: 08.02.2025).
28. Pytorch LSTMs for time-series data. Towardsdatascience.com. [Электронный ресурс]. URL: https://towardsdatascience.com/pytorch-lstms-for-time-series-data-cd16190929d7/ (дата обращения: 10.02.2025).
29. Scikit-learn. [Электронный ресурс]. URL: https://scikit-learn.org/stable/ (дата обращения: 08.02.2025).
30. Seaborn для визуализации данных в Python. Pythonru.com. [Электронный ресурс]. URL: https://pythonru.com/biblioteki/seaborn-plot (дата обращения: 07.02.2025).
31. Simple Linear Regression: Everything You Need to Know. Datacamp.com. [Электронный ресурс]. URL: https://www.datacamp.com/tutorial/simple-linear-regression (дата обращения: 09.02.2025).
32. Akperov I.G., Akperov G.I., Alekseichik T.V., Arapova E.A., Artamonova A., Aruchidi N.A., Andreeva O.V., Ansari M. et al. Soft models of management in terms of digital transformation. / Монография. Том. 2. - Rostov-on-Don: PEI HE SU (IUBIP), 2020. – 256 p.
33. Summary of LSTM Model. Discuss.pytorch.org. [Электронный ресурс]. URL: https://discuss.pytorch.org/t/summary-of-lstm-model/170608 (дата обращения: 10.02.2025).
34. XGBoost. [Электронный ресурс]. URL: https://xgboost.readthedocs.io/en/stable/ (дата обращения: 08.02.2025).
35. XGBRegressor vs. xgboost.train huge speed difference?. Stackexchange.com. [Электронный ресурс]. URL: https://datascience.stackexchange.com/questions/17282/xgbregressor-vs-xgboost-train-huge-speed-difference (дата обращения: 09.02.2025).
Страница обновлена: 09.03.2026 в 09:25:43
Download PDF | Downloads: 55
Gradient boosting algorithms versus recurrent networks in forecasting problems
Zhilina E.V., Efimova E.V., Tishchenko E.N.Journal paper
Informatization in the Digital Economy
Volume 6, Number 1 (January-March 2025)
Abstract:
Comparative analysis of machine learning methods and neural networks is an important tool for choosing optimal solutions, understanding their limitations and capabilities, as well as for developing new approaches and technologies in the field of artificial intelligence.
During development, the task of predicting time series based on electricity consumption readings is solved.
The authors have developed data forecasting algorithms using machine learning methods (gradient boosting of XGBoost, LightGBM and CatBoost, comparison of low-level and high-level interfaces xgb. train and XGBRegressor, and SimpleLinearModel), as well as using neural networks (recurrent networks implemented in Pytorch) in Python.
To analyze and evaluate the obtained results, model quality metrics (RMSE learning errors on training and test data) were calculated.
Based on the execution time of the training process of the developed models, a comprehensive comparison of algorithms (benchmarking) was performed.
The predicted values (real and calculated) were visualized.
Keywords: Python, ML, XGBoost, LightGBM, CatBoost, xgb.train, SimpleLinearModel, neural network, LSTM, Pytorch, benchmarking
JEL-classification: C40, C45, C49
References:
Akperov I.G., Akperov G.I., Alekseichik T.V., Arapova E.A., Artamonova A., Aruchidi N.A., Andreeva O.V., Ansari M. et al. (2020). Soft models of management in terms of digital transformation Rostov-on-Don: PEI HE SU (IUBIP).
Bagno A.S., Zhilina E.V. (2024). How artificial intelligence is changing teaching methods and student experience Rostov-on-Don: Rostovskiy gosudarstvennyy ekonomicheskiy universitet «RINKh».
LSTM for Time Series Prediction in PyTorchMachinelearningmastery.com. Retrieved February 08, 2025, from https://machinelearningmastery.com/lstm-for-time-series-prediction-in-pytorch/
LightGBM Classifier in PythonKaggle.com. Retrieved February 09, 2025, from http://kaggle.com/code/prashant111/lightgbm-classifier-in-python
LightGBM: A Highly Efficient Gradient Boosting Decision TreeProceedings.neurips.cc. Retrieved February 10, 2025, from https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf
Linear RegressionDatatab.net. Retrieved February 10, 2025, from https://datatab.net/tutorial/linear-regression
Long Short Term Memory (LSTM) Networks using PyTorchGeeksforgeeks.org. Retrieved February 08, 2025, from https://www.geeksforgeeks.org/long-short-term-memory-networks-using-pytorch/
Matplotlib. Retrieved February 07, 2025, from https://matplotlib.org/
Nikiforenko D.A., Karapetyan A.A., Efimova E.V. (2023). Application of machine learning and artificial intelligence in data analysis and digitalization of business processes New directions of scientific thought. 502-505.
NumPy. Retrieved February 06, 2025, from https://numpy.org/
Pandas. Retrieved February 06, 2025, from https://pandas.pydata.org/
Parameterize XGBoost with xgboost.train for regressionKaggle.com. Retrieved February 09, 2025, from https://www.kaggle.com/discussions/general/197091
Popov D.N., Zhilina E.V., Petrenko V.I. (2022). R-CNN approach to object recognition. Informatization in the Digital Economy. 3 (4). 211-220. doi: 10.18334/ide.3.4.115222.
PyTorchWikipedia.org. Retrieved February 08, 2025, from https://ru.wikipedia.org/wiki/PyTorch
Pytorch LSTMs for time-series dataTowardsdatascience.com. Retrieved February 10, 2025, from https://towardsdatascience.com/pytorch-lstms-for-time-series-data-cd16190929d7/
Scikit-learn. Retrieved February 08, 2025, from https://scikit-learn.org/stable/
Simple Linear Regression: Everything You Need to KnowDatacamp.com. Retrieved February 09, 2025, from https://www.datacamp.com/tutorial/simple-linear-regression
Sklyarov A.V., Tischenko E.N., Efimova E.V., Zhilina E.V. (2019). Assessment of efficiency of actions of information security on the protected economic systems with application of artificial neural networks. Economic sciences. (177). 77-81. doi: 10.14451/1.177.77.
Summary of LSTM ModelDiscuss.pytorch.org. Retrieved February 10, 2025, from https://discuss.pytorch.org/t/summary-of-lstm-model/170608
Veryutina V.V., Dzyuba A.G., Zhilina E.V. (2022). Segmentation of the customer base using the k-means method Problems of design, application and security of information systems in the digital economy. 50-55.
XGBRegressor vs. xgboost.train huge speed difference?Stackexchange.com. Retrieved February 09, 2025, from https://datascience.stackexchange.com/questions/17282/xgbregressor-vs-xgboost-train-huge-speed-difference
XGBoost. Retrieved February 08, 2025, from https://xgboost.readthedocs.io/en/stable/
Zhilina E.V., Efimova E.V., Rutta N.A., Savskaya A.R. (2020). Neuro- fuzzyapproach to forecasting information security risks in a university. Intellektualnye resursy - regionalnomu razvitiyu. (2). 132-137.
Zhukov A.V., Zhilina E.V. (2021). Models and algorithms for generating synthetic datasets for ML. Informatization in the Digital Economy. 2 (3). 95-102. doi: 10.18334/ide.2.3.113388.
