Two-factor labor supply functions at the macro level: a topic with variations

Введение

Предлагаемая работа преследует две цели. Первой целью является апробация предложенного в статье Е.Ф. Винокурова и Н.А. Винокуровой [1] подхода к построению функции предложения труда на макроуровне. Вторая цель – сравнительный анализ нескольких вариантов этой функции: построенных, во-первых, с использованием метода наименьших квадратов и, во-вторых, – описанным в публикациях Е.Ф. Винокурова [2] и [3] нестандартным методом.

В условиях сложившегося в последнее время в российской экономике дефицита рабочей силы проблема увеличения предложения труда благодаря росту экономической активности населения становится, чего несколько лет назад мало кто ожидал, крайне актуальной.

В то же время анализ рынка труда с позиций экономической теории является для современных экономистов непопулярным направлением исследований. Величина предложения труда и заработная плата обычно рассматриваются отдельно друг от друга. При обсуждении проблемы предложения труда акцент чаще всего делается на влияющие на него незарплатные факторы, прежде всего, демографию , а заработная плата анализируется либо в контексте уровня жизни, либо как элемент издержек производства. При этом вопрос о взаимосвязи этих показателей, т.е. о функции предложения, не ставится. Приведем несколько примеров. Предложение труда в России и других странах рассматривается в публикациях Р.И. Капелюшникова и А.Ю. Ощепкова [5], Н.Н. Подольной [11], О.П. Чекмарева О.П., А.Л. Ильвес А.Л. и П.А. Конева [14], О.А. Колесникова, Е.В. Маслова и И.В. Околелых [7], Р.Т. Утаралиевой [13], обзорах [10], [12], [15]. Ситуация с заработной платой в современной России описана в статьях Л.А. Миграновой [8], [9] и обзоре [15].

В настоящей статье рассматриваются построенные на базе динамических рядов двухфакторные функции предложения труда, имеющие вид

S=0,01N*f(W), (1)

где S – величина предложения труда (численность экономически активного населения, или рабочая сила),

W – реальная начисленная заработная плата,

f(W) – регрессионное уравнение, связывающее выраженный в процентах уровень экономической активности некоторой когорты населения с реальной заработной платой,

N – численность рассматриваемой когорты населения.

Таким образом, в (1) значение функции S зависит от значений двух факторов – W и N.

Расчеты по двухфакторной функции предложения труда вида (1) проведены и описываются впервые.

Функцию f(W) будем называть, как в упомянутой выше статье [1], модифицированной функцией предложения труда. Значение этой функции можно интерпретировать как выраженную в доле человеко-года величину предложения трудовых услуг в течение года усредненным индивидуумом, входящим в рассматриваемую когорту населения.

Именно при построении модифицированной функцией предложения труда в статье автора [3] впервые на практике был применен нестандартный подход к определению параметров уравнения регрессии, являющегося данной функцией. Суть этого подхода заключается в использовании при оценке данных параметров абсолютных значений отклонений теоретических значений функции от наблюдаемых. Такой подход представляется логичным, поскольку его применение базируется на величинах, имеющих ясную интерпретацию. В то же время квадраты отклонений, лежащие в основе метода наименьших квадратов и ряда других методов математической статистики, не имеют ни физического, ни экономического, ни какого-либо другого смысла, исключая абстрактно-математический. Использование при определении параметров уравнения регрессии величин, возведенных во вторую степень, как указывалось в статьях Е.Ф. Винокурова [2] и [3], было введено в практику из соображений реализуемости решения проблемы – соображений, ставших неактуальными после появления компьютеров.

Варианты модифицированной функции предложения труда

При классическом подходе, когда используется метод наименьших квадратов, значения параметров уравнения регрессии определяются исходя из критерия

- )²→min. (2)

Здесь

n – число наблюдений;

у_i – i-ое наблюдаемое значение результирующего признака;

– i-ое теоретическое значение результирующего признака.

В нашем конкретном случае n – это количество лет, за которое рассматриваются значения фактора и результирующего признака (i=1, 2, …, n), а результирующим признаком является уровень участия населения в рабочей силе.

В работе Е.Ф. Винокурова [3] было предложено заменить (или дополнить) расчеты на основе этого критерия определением параметров уравнений регрессии, базируясь на критериях

(3)

max (4)

или

max 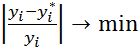. (5)

Критерий (3) представляет собой формализацию требования обеспечить минимум суммы модулей отклонений теоретических значений зависимой переменной от наблюдаемых. Представляется, что имеют право на существование и определяющие выбор параметров уравнения регрессии критерии (4) и (5). Критерий (4) требует минимизации максимального модуля отклонений теоретических значений зависимой переменной от наблюдаемых, а критерий (5) – минимизации модуля максимального относительного (к наблюдаемому значению) отклонения.

Параметры уравнений регрессии, обеспечивающие выполнение условий (3)-(5), определяются путем простого подбора из множества рассматриваемых их комбинаций.

В настоящей работе речь пойдет о четырех вариантах функции f(W), т.е модифицированной функции предложения труда. Переменными в этой функции, как указывалось выше, выступают значения реальной среднемесячной начисленной заработной платы за ряд лет, а значениями функции – уровень экономической активности населения в соответствующем году. В дальнейшем расчеты, базирующиеся на критериях (2), (3), (4) и (5), будем обозначать как варианты I, II, III и IV соответственно.

Экспериментальные расчеты, описываемые в статье, были проведены автором на примере российского рынка труда, причем рассматривался только учитываемый официальной статистикой «белый» рынок. В качестве исходной информации использованы динамические ряды предоставляемых Росстатом данных за период 2001-2014 гг. Базовым годом в динамическом ряде реальной среднемесячной начисленной заработной плате является 2008 г. Использованные для расчетов исходные данные представлены в табл. 1. Там же приведены значения численности населения в возрасте 15-72 лет, являющейся вторым фактором функции предложения труда (1) и – для сравнения с полученными нами теоретическими значениями – наблюдаемая численность рабочей силы.

Заметим, что до 2017 г. уровень участия в рабочей силе по рекомендациям Международной организации труда рассчитывался именно для учитываемой в наших расчетах возрастной когорты.

Таблица 1

Исходная информация для расчетов

Выбранный для апробации рассматриваемой методики построения функции предложения труда период определился несколькими обстоятельствами. Нижняя граница этого периода – это год, начиная с которого можно говорить о том, что в России устойчиво сформировался рынок труда. Этот факт отмечен, в частности, в работе автора [2] . Период завершается 2014 годом, поскольку экономический кризис 2015 года, как оказалось, привел к существенному изменению соотношения заработной платы и уровня экономической активности по сравнению с предыдущими годами, (что любопытно, в отличие от кризиса 2009 года). Но в любом случае динамические ряды невозможно было бы продлить далее 2016 г., т.к. начиная с 2017 г. изменилась методика определения численности экономически активного населения, и связанные с этой величиной показатели стали несопоставимыми с рассчитанными ранее. Впрочем, поскольку, как указывалось выше, данная статья носит методический характер, выбор временного интервала для апробации предлагаемой методики не имеет принципиального значения.

Анализ приведенных в табл. 1 данных показывает, что между уровнем участия в рабочей силе и реальной заработной платой наблюдается ярко выраженная положительная связь, носящая линейный характер. Этот факт хорошо иллюстрирует поле корреляций, представленное на рис. 1.

Указанное обстоятельство стало основанием для рассмотрения функции f(W) (модифицированной функции предложения труда) во всех вариантах как линейной.

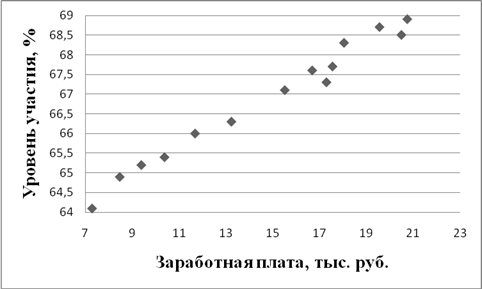
Рис. 1. Связь участия в рабочей силе с реальной заработной платой

Источник: составлено автором.

Расчеты вывели на следующие четыре варианта функции предложения труда на макроуровне f(W).

Вариант I.

у=0,332W+61,95. (6)

Вариант II.

у=0,335W+61,95. (7)

Вариант III.

у=0,340W+61,90. (8)

Вариант IV.

у=0,335W+62,00. (9)

Здесь у – уровень экономической активности населения в возрасте 15-72 лет в процентах.

Отметим, что построенное классическим методом уравнение регрессии (6) характеризуется весьма высоким коэффициентом детерминации, равным 0,98. Как видно из формул (6)-(9), построенные нами функции различаются незначительно, на основании чего можно полагать, что и функции (7)-(9) достаточно адекватно описывают реальность.

Хотя различия между функциями (6)-(9) невелики, тем не менее, интересно эти функции сопоставить. Сопоставление представляется логичным провести по трем определяемым критериями (3)-(5) характеристикам этих функций. Такими характеристиками являются сумма модулей отклонений теоретических значений уровня экономической активности населения от наблюдаемых – , максимальное отклонение модуля теоретических значений функции от наблюдаемых – max и максимальное относительное отклонение модуля теоретических значений функции от наблюдаемых – max .

Значения этих трех характеристик для всех четырех вариантов функции у= f(W) приведены в табл. 2.

Таблица 2

Характеристики модулей отклонений теоретических значений

уровня экономической активности населения от наблюдаемых

Из табл. 2 видно, что, как и можно было ожидать, характеристики всех четырех рассмотренных вариантов модифицированной функции предложения труда близки между собой.

Варианты двухфакторной функции предложения труда

Получив выражения для модифицированных функций предложения труда, естественно, оказалось несложным по формуле (1) рассчитать теоретические значения численности экономически активного населения S в четырех вариантах:

Вариант I.

S=0,01N*(0,332W+61,95). (10)

Вариант II.

S=0,01N*(0,335W+61,95). (11)

Вариант III.

S=0,01N*(0,340W+61,90). (12)

Вариант IV.

S=0,01N*(0,335W+62,00). (13)

В таблице 3 приведены выраженные в процентах относительные отклонения полученных теоретических значений величин предложения труда от наблюдаемых. Из этой таблицы видно, что во всех вариантах полученные функции S(y, N) достаточно адекватно отображают реальность. Лишь в 2001 г. модули относительных отклонений теоретических значений численности экономически активного населения от наблюдаемых превышают 1%.

Таблица 3

Относительные отклонения теоретических значений

величин предложения труда от наблюдаемых, %

Правда, если провести анализ этих отклонений по той же схеме, по которой был проведен анализ отклонений теоретических значений уровня участия в рабочей силе от наблюдаемых, то мы получаем, если не обескураживающий, то несколько неожиданный результат (см. табл. 4).

Из табл. 4 выясняется, что наилучшим из четырех вариантов двухфакторной функции предложения труда с позиций всех трех рассматриваемых характеристик оказывается вариант I – вариант, базирующийся на признанной нами нелогичной функции (6). Правда, нужно отметить, что суммы модулей отклонений для этого варианта и варианта II различаются всего на 2 тыс. чел., что можно считать в данном случае пренебрежимо малой величиной.

Таблица 4

Характеристики модулей отклонений теоретических значений

численности экономически активного населения от наблюдаемых

Хотя проведенные расчеты, как было указано выше, являются экспериментальными, и автор не настаивает на абсолютной точности полученных результатов, результаты эти нуждаются в объяснении. Объяснение это сводится к тому, что на предложение труда, кроме заработной платы и численности рассматриваемой возрастной когорты населения влияют и многие другие факторы, не учтенные в рассматриваемой модели. К числу этих факторов относятся численность молодежи и другие демографические характеристики, ситуация в образовательной сфере, определенный законом пенсионный возраст, число призываемых на службу в вооруженных силах и установленные законом сроки службы, нормы законодательства, определяющие размеры пособия по безработице и право на его получение, доходы населения, получаемые в виде трансфертов, миграционные процессы и т.д. Эти факторы подробно рассмотрены в публикациях Р.И. Капелюшникова и А.Ю. Ощепкова [5], Н.Н. Подольной [11], Е.Ф. Винокурова [4]. Надо полагать, что именно неучтенные в уравнениях вида (1) факторы в определенной степени обусловили полученные в результате расчетов по формулам (10)-(13) результаты.

Заключение

Проведенное исследование показало принципиальную возможность построения нескольких вариантов достаточно адекватных функций предложения труда на макроуровне, каждый из которых имеет право на существование. В такой ситуации перед исследователем в зависимости от цели исследования встает вопрос либо о выборе одного из них, либо о формировании некоторого компромиссного варианта. Логика такого рода решений – это одно из направлений дальнейшей работы.

Представляется целесообразным также разработать алгоритмы определения верней и нижней границы для каждого параметра уравнения регрессии, являющегося модифицированной функцией предложения труда, что позволило бы сократить объем расчетов, необходимых для определения их значений на основе критериев (3), (4) и (5).

Отдельная проблема – разработка показателя, оценивающего, насколько адекватно полученные на основе рассмотренных в статье критериев уравнения регрессии отражают реальность, – показателя, являющегося аналогом коэффициента детерминации при использовании классических статистических методов.

И, наконец, предложенный в работе подход к построению уравнений регрессии требует разработки соответствующего программного обеспечения.