Multi-projection optimization model for comparative assessment of economic systems

Введение. Компаративному анализу экономических систем и выбору предпочтительных альтернатив всегда придавалось исключительно важное значение в науке и практике [15; 32; 33]. В экономических исследованиях под системами понимается обширное множество систем (как объектного, так и проектного типов) на макро-, мезо- и микроуровнях – начиная со стран и их объединений и заканчивая бизнес-единицами и отдельными инвестиционными проектами [9–11]. Такого рода оценку осуществляют различные стейкхолдеры (заинтересованные стороны): представители профильных государственных, региональных и муниципальных органов, собственники, менеджеры, инвесторы, кредиторы и иные участники экономических отношений [15; 28; 29].

Комплексную оценку состояния экономических систем, как правило, обеспечивает использование совокупности показателей, объединенных в соответствующие группы (проекции) [1; 7; 27]. Сложность такого выбора обусловлена противоречивостью показателей как внутри проекций, так и между ними [8; 12]. Для раскрытия неопределенности разработан профильный научно-методический аппарат. Принципы, методы и методики многопроекционного и многокритериального выбора известны [23–25]. В данной статье реализована их интеграция в рамках единой оптимизационной модели.

Описание модели. Модель многопроекционной сравнительной оценки состояния экономических систем приведена на рисунке 1. На переднем плане изображен блок, раскрывающий сопоставление систем в некоторый актуальный момент времени. Базис модели составляют профильные методы многопроекционного выбора (анализ-синтез, кластеризации, исключения проекций и главной проекции), а также научно-методический аппарат классического многокритериального выбора [20; 21; 24]. Указанные компоненты отражены в головной (верхней) части многопроекционной модели.

Руководствуясь собственными целями Ц = {Ц_i}, в области обеспечения устойчивости, безопасности, инновационности, эффективности и пр. [6; 26; 30], стейкхолдер определяет состав сравниваемых экономических систем S = {S_i}, и показателей К = {Кⁱ_j}, , . Показатели имеют двойную нумерацию: верхний индекс i обозначает номер проекции, а нижний j – номер показателя в ней. Согласно рис. 1 изначально осуществляется многокритериальный анализ в проекциях.

Многопроекционное решение синтезируется посредством пересечения оптимальных множеств проекций [24; 25], полученных на базе лучших систем (1), эффективных вариантов (2), альтернатив нижестоящих рангов (3):

, (1)

, (2)

. (3)

Выражения (1)–(3) описывают симметричный выбор. Кроме того, возможен асимметричный выбор в соответствии с формулой (4), когда задействуемые для синтеза проекционные множества различаются:

. (4)

Тем самым реализуется широкое многообразие возможностей классического, а также жесткого либо мягкого (как симметричного, так и асимметричного) выбора. Допустимо принятие одной из проекций за главную, что приводит к многокритериальному выбору. Оптимизационные расчеты начинаются с выделения первого кластера и распространяются далее на нижестоящие кластеры по мере необходимости. Таким образом, модель позволяет выявить пространственно-временную структуру сравниваемых систем. В процессе решения исследовательских задач возможно рассогласование априорного видения стейкхолдерами состава и количества кластеров на стадии постановки задачи с результатами моделирования.

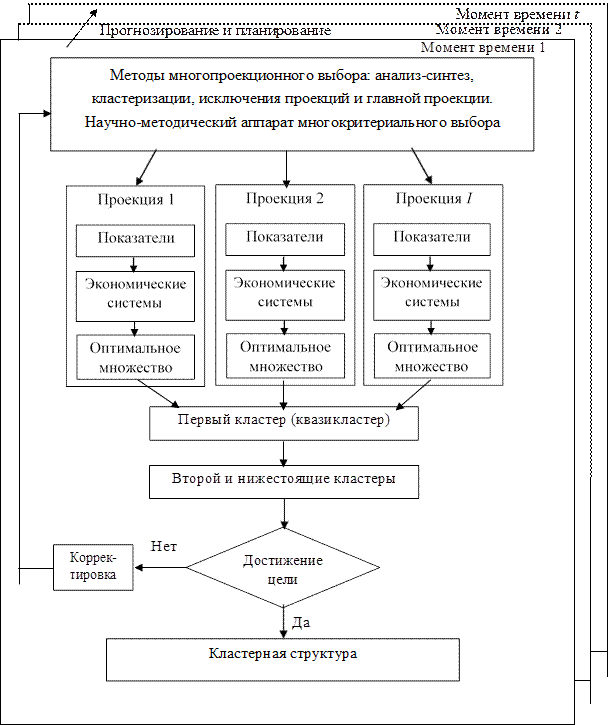
Рисунок 1. Модель многопроекционной сравнительной оценки

состояния экономических систем

Источник: составлено автором.

Устранение когнитивного диссонанса осуществляется путем корректирующих воздействий. Могут пересматриваться состав систем, показателей, проекций, набор принципов и методов оптимизации, инструментарий прогнозирования, планирования и импутации данных, момент времени проведения исследования, исходная цель [24; 25]. Чтобы перейти к будущему моменту времени, следует осуществить надлежащее прогнозирование (планирование) состояния. При этом недопустимы манипуляции в интересах выхода на желаемый результат вопреки научно обоснованному.

Моделирование. Поясним специфику многопроекционного оптимизационной модели двумя характерными примерами. Полагаем, что требуется определить лучшую экономическую систему из десяти S₁–S₁₀ в двухпроекционной постановке. Изначально обратимся к точечному выбору, описываемому формулой (1).

Построчно упорядоченные по мере улучшения значений показателей номера 1–10 сравниваемых экономических систем представим в виде сортированных массивов.

Рассмотрим выбор лучшей альтернативы в первой проекции.

Следуя рекомендациям [23], находим опорные варианты с номерами 5, 10 и 6 – крайние правые элементы в сортированном массиве (выделены жирным шрифтом).

По второму показателю альтернативу 5 превосходят варианты 2 и 10, а по третьему – 2, 6 и 10. С улучшением двух показателей приходим к приемлемому множеству М₅ = {S₂, S₁₀}.

По первому показателю альтернативу 10 превосходит вариант 5, а по третьему – 6. С улучшением двух показателей переход невозможен, следовательно, М₁₀ = {S₁₀}.

По первому и второму показателям альтернативу 6 превосходят варианты 2, 5 и 10. Получим М₆ = {S₂, S₅, S₁₀}.

Посредством пересечения промежуточных множеств формируем единственное решение в первой проекции М¹_т = {S₂, S₁₀}∩{S₁₀}∩{S₂, S₅, S₁₀} = {S₁₀} (в сортированном массиве обозначено курсивом).

Обратимся ко второй проекции.

Здесь не приводя текстового описания ограничимся логической схемой.

Единственное решение во второй проекции имеет вид – М²_т = {S₉}.

Согласно формуле (1) первый кластер не сформирован: М_1КЛ = {S₁₀}∩{S₉} = Ø. В таких условиях логичным становится задействование эффективных множеств и обращение к формуле (2) [24; 25].

Построение эффективного множества в первой проекции [15].

Построение эффективного множества во второй проекции.

Множество эффективных систем во второй проекции М²_эф = {S₁, S₆, S₉}.

Руководствуясь выражением (2), синтезируем первый кластер – М_1КЛ = {S₅, S₆, S₁₀}∩{S₁, S₆, S₉} = {S₆}.

Таким образом, реализованный в оптимизационной модели переход от максимально жесткого точечного выбора в проекциях к более умеренному паретовскому выбору способствовал формированию кластера.

Обратимся к асимметричному выбору согласно формуле (4). Имеем М¹_т = {S₁₀}, М²_эф = {S₁, S₆, S₉} и М¹_эф = {S₅, S₆, S₁₀}, М²_т = {S₉}. Здесь в обоих случаях синтез двухпроекционных решений неосуществим – М_1КЛ = {S₁₀}∩{S₁, S₆, S₉} = Ø и М_1КЛ = {S₅, S₆, S₁₀}∩{S₉} = Ø.

Далее рассмотрим пример поиска компромисса на уровне эффективных множеств в рамках оптимизационной модели.

Построение эффективного множества в первой проекции.

Множество эффективных систем в первой проекции М¹_эф = {S₆, S₉, S₁₀}.

Построение эффективного множества во второй проекции.

Множество эффективных систем во второй проекции М²_эф = {S₃, S₈}.

На базе формулы (2) посредством пересечения частных множеств двух проекций первый кластер не сформирован – М_1КЛ = {S₆, S₉, S₁₀}∩{S₃, S₈} = Ø.

В соответствии с оптимизационной моделью при отсутствии компромисса на уровне паретовских множеств привносим в анализ вторые ранги и задействуем квазиэффективные множества согласно формуле (3).

В первой проекции анализу подлежат альтернативы S₁–S₅, S₇ и S₈.

Построение множества второго ранга в первой проекции.

Доминирует вариант 8, имеем М¹_2р = {S₈} и квазиэффективное множество – М¹_кэф = {S₆, S₈, S₉, S₁₀}.

Во второй проекции остается сопоставить альтернативы S₁, S₂, S₄–S₇, S₉ и S₁₀.

Построение множества второго ранга во второй проекции. Итерация 1.

Итерация 2.

Множество систем второго ранга во второй проекции М²_2р = {S₁, S₂, S₆, S₇, S₉}, а квазиэффективное множество – М²_кэф = {S₁, S₂, S₃, S₆, S₇, S₈, S₉}.

Руководствуясь формулой (3), путем пересечения оптимальных множеств синтезируем первый квазикластер – М_1КВ = {S₆, S₈, S₉, S₁₀}∩{S₁, S₂, S₃, S₆, S₇, S₈, S₉} = {S₆, S₈, S₉}. Следовательно, осуществленный в рамках модели переход от классического паретовского выбора в проекциях к более мягкому квазивыбору привел к многопроекционному результату.

Наряду с этим возможны два асимметричных решения, полученных на базе выражения (4). Известно, что М¹_эф = {S₆, S₉, S₁₀} и М²_кэф = {S₁, S₂, S₃, S₆, S₇, S₈, S₉}, тогда М_1КВ = {S₆, S₉, S₁₀}∩{S₁, S₂, S₃, S₆, S₇, S₈, S₉} = {S₆, S₉}. Соответственно при М¹_кэф = {S₆, S₈, S₉, S₁₀} и М²_эф = {S₃, S₈} синтезируем М_1КВ = {S₆, S₈, S₉, S₁₀}∩{S₃, S₈} = {S₈}.

Аналогичным образом далее могут быть выделены нижестоящие кластеры (квазикластеры). Суть модели ясна.

Заключение

Изложенная оптимизационная модель займет ключевое место в теории и методологии многокритериального и многопроекционного выбора и будет полезна при формировании профильных подходов, моделей, классификаций, методик и алгоритмов для изучения широкого круга экономических систем на различных иерархических уровнях при решении насущных задач оценки устойчивости [18; 19; 31], безопасности [3; 5; 13], инновационности [14; 16; 17] и эффективности [2; 4; 22] основными заинтересованными сторонами в лице руководителей (представителей) министерств, ведомств и департаментов, собственников, менеджмента, инвесторов, кредиторов и других участников экономических отношений.