Economic and mathematical modeling of mining conditions and prospects

Введение

Последнее десятилетие характеризуется серьезной динамикой социально-экономического развития в нашей стране. Большое внимание уделяется развитию специфических особенностей региональной экономики, направленных на повышение качества жизни населения. В современных исследованиях рассматриваются экономико-математические методы и математические модели, позволяющие прогнозировать экономические показатели (методы индексной оценки [5], математического моделирования [6], [9], [14], комбинаторные методы [13]).

В настоящее время вышел целый ряд работ о математических моделях, связанных с вопросами состояния, перспектив и добычи полезных ископаемых, некоторые из них отражены в статьях [10], [16], [17]. В работах [2], [3], [4] дан обзор состояния исследований и предложена модель по типу производственной функции, на 68% объясняющая зависимость добычи полезных ископаемых относительно стоимости основных фондов, а также численности занятых в рассматриваемой отрасли. Авторами уточняется, что точность модели в виде средней ошибки аппроксимации сохраняется на уровне 58%. Однако применив процесс линеаризации, ими показано, что коэффициент детерминации повышается до 87%, а точность в виде средней ошибки аппроксимации ориентируется уже на 8%. Таким образом, линейная модель довольно хорошо описывает фактические данные.

Цель исследования заключается в изучении вопросов математического моделирования, связанных с добычей полезных ископаемых, а также комбинаторных методов с точки зрения их возможного использования в экономическом анализе региона.

Методы исследования

Основным материалом исследования являются данные Федеральной службы государственной статистики [8]. В качестве основных методов выбраны методы описательной статистики, эконометрического моделирования, в частности, используется построение линейных регрессионных моделей. Еще одним перспективным, по мнению авторов, представляется комбинаторный метод.

Результаты

Покажем, что линейные модели могут быть самостоятельно использованы для анализа связей при изучении добычи полезных ископаемых. Например, по данным статистики за 2020-2023 годы [8], рассмотрим зависимость индекса предпринимательской уверенности и общего спроса на продукцию в таблице 1. Заметим, что индекс предпринимательской уверенности в добыче полезных ископаемых рассчитывается как среднее арифметическое значение балансов оценок уровней спроса (портфеля заказов), запасов готовой продукции (с обратным знаком), а также ожидаемого выпуска продукции (расчет производится с учетом Официальной статистической методологии расчета показателей «Индекс предпринимательской уверенности», утвержденной приказом Росстата от 14 сентября 2022 года № 643).

Таблица 1 – Индекс предпринимательской уверенности (y) и общий спрос на продукцию (x) в 2020-2023 гг.

Уравнение регрессии имеет вид: y=6,93+0,42x, где у – индекс предпринимательской уверенности, а х – спрос на продукцию, так называемый портфель заказов. Коэффициент детерминации составляет 80%, статистически значим. Средняя ошибка аппроксимации составляет 5%, что показывает хорошее качество модели. Конечно, такая зависимость ожидаема, ее детальный анализ показывает, что линейная связь описывается на 90%. Соответствующее графическое представление отражено на рисунке 1:

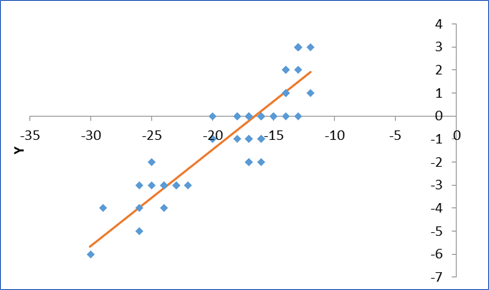
Рисунок 1. Зависимость индекса предпринимательской уверенности от спроса,

2020-2023 гг.

Источник: составлено авторами по результатам исследования

Рассмотрим многофакторную модель y=a+b₁x₁+b₂x₂+b₃x₃+b₄x₄+b₅x_5, где y – средний уровень используемых мощностей, x₁ – численность занятых, x₂ – спрос на продукцию на внешнем рынке, x₃ – запасы готовой продукции, x₄ – выпуск основного вида продукции, x₅ – общий спрос на продукцию. Данные [9] для построения многофакторной модели представлены в таблице 2. Заметим, что с января 2017 года при проведении обследований используется Общероссийский классификатор видов экономической деятельности [7].

Таблица 2 – Данные для построения многофакторной модели среднего уровня используемых производственных мощностей в 2020-2023 гг.

Наиболее высокий уровень использования производственных мощностей в России был в 2020 г., несмотря на эпидемию COVID-19, и составлял 64-65%. В последующие годы использование производственных мощностей снизилось, но в 2023 г. снова появилась тенденция к увеличению использования производственных мощностей, особенно это стало заметным к концу 2023 г. Тенденции использования производственных мощностей в течение года за период 2020-2023 гг. отражены на рисунке 2:

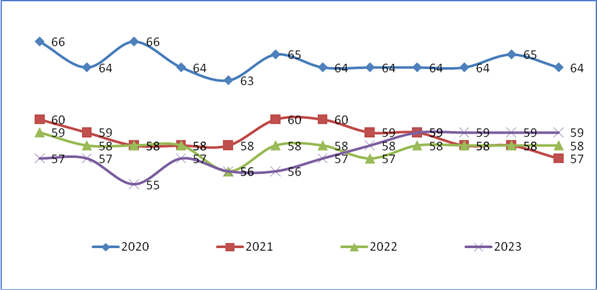
Рисунок 2. Изменение уровня использования производственной мощности в России в 2020-2023 гг., %

Источник: составлено авторами по результатам исследования

Приведенные в таблице 2 данные, описывают следующую линейную модель: y=54,6-0,43x₁+0,50x₂+0,29x₃+0,008x₄-0,73x₅. При этом наблюдается невысокая линейная зависимость между выпуском основного вида продукции и общим спросом на продукцию, однако это не приводит к мультиколлинеарности и дальнейший анализ не уменьшает число переменных.

Коэффициент детерминации такой модели 90%. Средняя ошибка аппроксимации составляет 2%. Модель хорошо описывает фактические данные и может быть использована в экономическом анализе. В частности, на основе модели можно сделать выводы, что использование производственной мощности в большей степени увеличивается при увеличении спроса на продукцию на внутреннем и внешнем рынке. Линейные модели, как известно, используются и при изучении изменений признаков во времени, как правило, при построении трендов. Такой подход проявляет себя особенно наглядно.

В последнее время вышел ряд работ о комбинаторном методе в исследованиях некоторых экономических показателей, в частности, в конструировании будущего территориальных образований [13]. Предлагается «мягкий» комбинаторный метод. В основу метода положен ряд принципов, который, на наш взгляд, имеет более широкое применение.

Первый принцип – принцип стратегической сборки интегрального вектора развития территории в пространстве ключевых направлений, реализуемый посредством формул. Такой вектор направлений легко может быть перенесен на изучение вопросов, связанных с добычей полезных ископаемых. Для этого необходимо определить ключевые направления исследуемой области и их весовые коэффициенты Интегральный вектор, следуя, представляет собой сумму произведений ключевых направлений на их весовые оценки. Данный подход может найти свое применение в вопросах планирования и позволяет увидеть будущую траекторию. Говоря о принципе трансформационных изменений, необходимо провести анализ текущего состояния, определить будущее состояние и переходное, позволяющее перейти от текущего к будущему.

Принцип причастности базируется на привлечении к процессам планирования максимального числа заинтересованных лиц. Анализ в добывающей области может рассматриваться как движение по вектору посредством выполнения ряда конкретных проектов (аналогом выступает проектная дорожная карта). Сборка вектора может быть проведена аналогично работе, где проводится анализ двух векторов: вектора развития территории СВ и вектора развития её территориального окружения СЕ, что позволяет выявлять и решать проблемы, возникающие при внешней интеграции. Если заинтересованные лица, задействованные в вопросах планирования, обладают знаниями эконометрического моделирования, то такой подход, по нашему мнению, является оптимальным.

Если проанализировать наши предыдущие исследования, то нетрудно видеть, что конструкция интегрального вектора представляет собой не что иное, как линейную модель определенного вида, где в качестве переменных выступают ключевые направления, а коэффициенты при переменных – весовые оценки. В рассмотренном выше примере можно в качестве ключевых направлений положить направления, соответствующие переменным x₁, x₂, x₃, x₄, x₅, а полученные методом наименьших квадратов оценки коэффициентов регрессии принять, например, за весовые оценки.

Комбинаторные методы, особенно в сочетании с классическими и мягкими подходами, имеют широкие перспективы. В настоящий момент авторами рассматривается перенос некоторых комбинаторных свойств объектов на всевозможные их расширения подобно тому, как это происходит в комбинаторной теории групп.

Рассмотрим некоторые теоретические вопросы комбинаторной теории групп с точки зрения их возможного использования в экономическом анализе региона. Особый интерес среди таких вопросов представляет изучение алгоритмических характеристик групповых конструкций. Алгоритмическими являются такие свойства конструкций как равенство и сопряженность входящих в эти конструкции элементов, а также ряд других. Такие характеристики впервые введены М. Дэном, причем особый интерес представляет перенос этих характеристик с составляющих конструкций на общую структуру. В общем случае деновские свойства не выполняются, так как существуют составляющие групповых конструкций с их отсутствием, что показано выдающимся алгебраистом П.С. Новиковым. Построенный им пример группы, заданной множеством из конечного числа порождающих и конечного числа определяющих элементов, доказывает существование групп, в которых не существует алгоритм проверки равенства слов, и, кроме того, не существует эффективного способа проверки сопряженности. Однако ряд комбинаторных свойств может быть перенесен с групп на групповые конструкции. Рассмотрим в качестве примера одно из таких свойств.

Определение 1. Будем говорить, что в группе Gподгруппа Aизолирована, если произвольный элемент обладает свойством: влечет выполнение условия: .

Определение 2. Пересечение подгрупп из группы G, каждая из которых содержит подгруппу A и изолирована в G, будем называть изолятором подгруппыA в группе G и обозначать .

Определение 3. Будем говорить, что в группе G выполнено свойство K, когда всякая подгруппа с конечным числом порождающих и определяющих элементов, обладает конечно порожденным изолятором .

Рассмотрим группу , т.е. − групповую конструкцию свободного произведения групп A₁и A₂, причем объединение ведется по изолированной подгруппе H=H₁= H_{2 ,} где H₁ – подгруппа из A₁и H₂ – подгруппа изA₂ .

Лемма 1. Пусть , где B_i<A_i, i=1,2, H’<H, B₁B₂ конечно порождены и изолированы. A_i, i=1,2, обладают свойством K, а подгруппа H удовлетворяет условию максимальности и изолирована. Тогда изолятор J(N) конечно порожден.

Лемма 2. Пусть конструкция является свободным произведением групп A₁ и A₂, объединенных по изолированной подгруппе H с условием максимальности. Тогда если в множителяхA₁ и A₂ выполняется свойство K, то оно выполняется в группе G. А теперь рассмотрим некоторые конкретные группы, удовлетворяющие условиям леммы 2.

Теорема. Пусть G₁,G₂ – двупорожденные группы Кокстера. В конструкции свободного произведения этих групп с объединением по циклической подгруппе, порождаемой образующим элементом этих групп, выполняется свойство K. Доказательство опирается на структуру групп Кокстера [1].

Из представленной задачи комбинаторной теории групп мы видим, как произошел перенос свойств конкретных групп на их групповые конструкции. Таким образом, происходит расширение тех или иных свойств на укрупненные структуры. По мнению авторов, такие подходы можно рассматривать и в экономическом анализе регионов.

Выводы

Рассмотренные вопросы моделирования, в особенности, связанные с линейными моделями, важны для изучения экономического развития и анализа экономических показателей, в частности, добывающей отрасли. Применение комбинаторных методов в экономическом анализе и планировании является весьма перспективным. Вопросы, связанные с групповыми конструкциями, встречающимися повсеместно, и их применениями, представляют интерес не только с комбинаторной точки зрения, позволяя расширять свойства на более общие структуры, но и с возможным применением в экономических исследованиях, что весьма актуально в условиях цифровизации [11], [12], [15].