General approach to the analysis of the dynamic systems' equilibrium in the economic sphere

Динамическую систему любого процесса, изменяющегося во времени, можно описать математической моделью в экономической сфере. Параметры модели зависят от времени, явно или неявно. Эта модель описывает процесс перехода системы из одного состояния в другое, характеризуется своим начальным состоянием и законом. Этот закон прогнозирует состояние динамической системы в последующие моменты времени, исходя из определенного начального состояния.

Методы качественной теории дифференциальных уравнений при решении задач взаимосвязанных экономических процессов позволяют описать характер поведения любой экономической динамической системы в вопросах устойчивости, положений равновесия и переходов от одного стационарного состояния к другому, а также проделать бифуркационный параметрический анализ для конкретной экономической задачи. Математическая модель, описывающая процесс взаимосвязи экономических объектов, есть автономная система дифференциальных уравнений.

Систему дифференциальных уравнений:

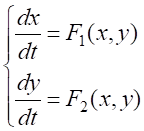, (1)

где функции в правой части аналитические на всей плоскости (x,y) и не содержат независимую переменную t, и называют автономной динамической системой второго порядка, а графики ее решения задачи Коши называют траекториями данной системы. Фазовый портрет определяют как множество траекторий системы (1) в некотором фазовом пространстве. Особые точки или положения равновесия динамической системы могут быть центром, устойчивым или неустойчивым узлом, устойчивым или неустойчивым фокусом. Особо отметим положение равновесия, называющееся седлом, в окрестности которого находится только конечное число траекторий. Эти траектории называются сепаратриссами. Характерное свойство сепаратрисс – это свойство связывать седло с фокусами, узлами и предельными циклами. Такое поведение сепаратрисс позволяет получить некий каркас фазового портрета динамической системы, при этом фазовое пространство делится на области, которые называются ячейками, причем внутри ячеек траектории ведут себя одинаково, т. е. или стягиваются к одному и тому же множеству на границе ячейки, или являются циклами. Бифуркационный анализ динамической системы позволяет установить параметрический портрет этой системы, а также бифуркационные границы, на которых происходит качественная перестройка фазового портрета.

В динамических системах процессы взаимосвязаны, и устойчивость систем характеризуется стремлением к положению равновесия, но практически не может полностью его достичь. Процессы в экономической сфере имеют, как правило, не только сложную динамическую структуру, но и с течением времени входят в состояние динамического хаоса, зависящего от начальных условий и некоторых флуктуаций внешней среды. В состоянии хаоса динамическая система теряет достоверность исходных прогнозов, в этом случае можно сказать, что малое отклонение от текущей траектории, как правило, приводит к очень значительному отклонению в следующий момент времени. В эволюционных процессах огромную роль играет теория бифуркаций.

Конкретные задачи в экономической сфере приведены в монографии Милованова В.П. [1] (Milovanov, 2001). В общем виде зададим некоторый экономический процесс системой (1). В этой системе (x, y) – изображающая точка, т.е. точка, которая определяет состояние системы в некоторый момент времени, фазовая траектория состоит из этих изображающих точек и показывает поведение системы как во времени, так и в окрестности положения равновесия. К динамической системе применяем метод Ляпунова [2, 3] (Bautin, Leontovich, 1976; Malkin, 1966) – метод исследования нелинейных систем в окрестности неподвижных точек. Этот метод (метод линейного приближения или метод линеаризации) позволяет выяснить устойчивость поведения экономической динамической системы в окрестности положения равновесия. Отметим, в окрестности этой точки портреты системы (1) и ее линеаризации эквивалентны, в случае, если неподвижная точка .

Положения равновесия системы (1) есть решения системы:

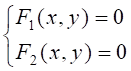
Линеаризованная система для системы (1) получается разложением в степенной ряд функций в правой части в окрестности положения равновесия (неподвижной точки) методом удержания линейных частей разложения:

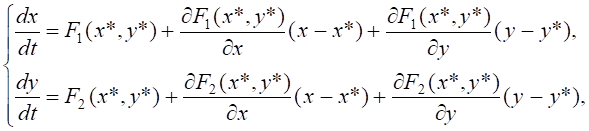
где ,

Матрица Якоби коэффициентов последней системы имеет вид:

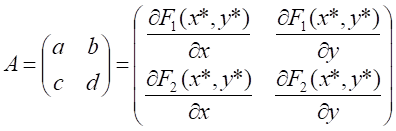(2)

Собственные числа матрицы (2) есть корни характеристического уравнения этой матрицы:

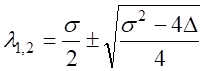, (3)

где параметры

след матрицы Якоби, а

– определитель матрицы Якоби.

Параметры и определяют каркас фазового портрета. В зависимости от их значений можем получить следующие особые точки: узел, фокус, седло, центр [4] (Riznichenko, 2002). При определенных сочетаниях и осуществляется переход через бифуркационные границы, в этом случае меняется тип фазовой траектории, а значит, характер фазового портрета качественно изменяется. Положения равновесия могут быть устойчивыми и неустойчивыми. Если все собственные числа матрицы Якоби A динамической системы имеют отрицательные вещественные части, то положение равновесия асимптотически устойчиво, а если хоть одно собственное число имеет положительную часть, то положение равновесия неустойчиво. Характер устойчивости точки меняется, как правило, при переходе через бифуркационные границы. Устойчивая система возвращается в состояние равновесия после удаления внешних сил, которые вывели ее из этого состояния.

Плоскость параметров и можно разбить координатными осями и параболой:

на области параметров с одинаковым характером положений равновесия (рис. 1) [4] (Riznichenko, 2002). Эти области параметров есть ячейки совокупности фазовых траекторий одинакового типа поведения в окрестности особой точки.

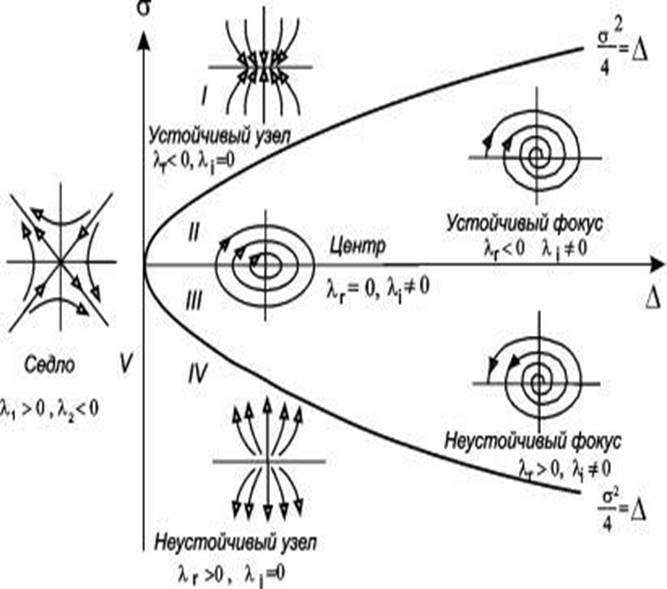
Рисунок 1. Разбиение плоскости на области с одинаковым характером положений равновесия

Источник: построено авторами по результатам исследования

Заключение

Исследуя нелинейную динамическую систему в экономической сфере, мы после бифуркационного анализа получим:

1) параметрический портрет поведения динамической системы,

2) решения, позволяющие оценить поведение системы во времени при конкретных параметрах,

3) определить бифуркационные значения параметров.

Некоторые результаты решений конкретных задач экономического поля получены в работах [5–11] (Kolesnikov, 2006; Bratishchev, 2017; Bratishchev, Batishcheva, Zhuravleva, 2019; Bratishchev, Batishcheva, Denisov, Zhuravleva, 2020; Zhuravleva, Lapina, 2013; Zhuravleva, Bratishchev, 2015; Zhuravleva, Kuznetsov, 2017).