Применение синергетических методов управления в исследовании динамической системы «Предложение и спрос»

Введение. Актуальность моделирования взаимосвязи спроса и предложения определяется тем, что в экономике важнейшими параметрами рынка являются спрос, предложение и равновесная цена, изменение соотношения между которыми вызывает колебания рыночных цен вокруг равновесной цены, следствием которых является формирование такого уровня цен, при котором достигается состояние равновесия спроса и предложения.

Материалы и методы. В работах [3, 16–18] (Bratishchev, Batishcheva, Zhuravleva, Guzenko, 2020; Bratishchev, Batishcheva, Zhuravleva, 2019; Bratishchev, Batishcheva, Denisov, Zhuravleva, 2020; Batishcheva, Zhuravleva, Rogozhin, 2022) с помощью качественной теории динамических систем [1, 4] (Bautin, Leontovich, 1990; Bratishchev, 2015) и теории синергетического управления [10] (Kolesnikov, 2006) исследованы нелинейные математические модели производства и обмена и управления посреднической деятельностью. Решение данных задач выполнено с помощью использования систем дифференциальных уравнений [2, 8] (Bakanov, Melnik, Sheremet, 2007; Gerasimov, Puchkov, Protasov, 2010), рассмотренных в работах В.П. Милованова [12–14] (Milovanov, 2001; Milovanov, 2010; Milovanov, 2011).

В настоящей статье для решения поставленной задачи моделирования динамической системы «Предложение и спрос» указанными выше методами рассматривается математическая модель, которая имеет вид [13] (Milovanov, 2010):

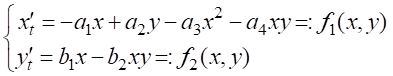. (1)

Здесь

предложение производителя, то есть количество товара, находящееся в распоряжении производителя в момент времени ;

спрос потребителя, то есть объем денежной массы потребителя, предназначенный для приобретения товара .

Скорость изменения (роста или снижения) предложения определяется в работе влиянием следующих четырех факторов:

моральная и физическая изнашиваемость товара;

наличие денежной массы у потребителя;

ухудшение качества выпущенного товара с течением времени;

раскупаемость товара.

Скорость изменения (роста или снижения) спроса определяется в работе влиянием следующих двух факторов:

количество товара у производителя;

сбыт товара.

Параметры предполагаются произвольными положительными числами.

Для исследования модели (1) авторами проведен полный бифуркационный анализ системы [1] (Bautin, Leontovich, 1990).

Результаты и обсуждение. Анализ конечных состояний равновесия. Исходя из экономического смысла в работе рассмотрена первая четверть фазовой плоскости.

Система (1) имеет 3 состояния равновесия:

.

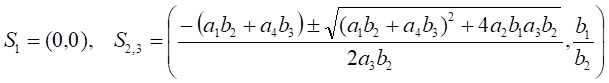Применив теорему Ляпунова об устойчивости по первому приближению [11] (Malkin, 1966), устанавливаем, что независимо от значений параметров всегда является седлом и грубым состоянием равновесия, – является грубым устойчивым узлом, а – грубым неустойчивым узлом. Этот результат подтверждается численно (рис. 1), построением с помощью математического пакета Matlab+Simulink фазового портрета в окрестности этих состояний для конкретных значений параметра [6, 7, 15] (Bratishchev, 2012; Vasilev, Simak, Rybnikova, 2008; Gerasimov, Regeda, Regeda, 2017).

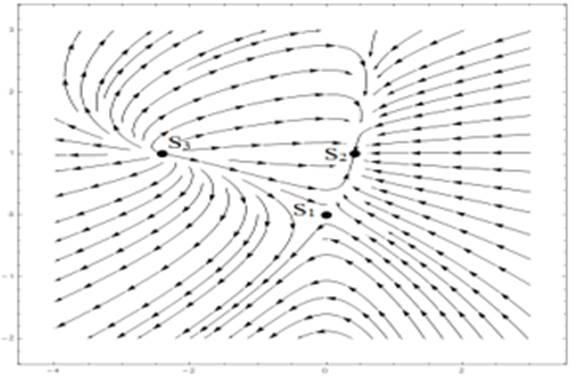
Рисунок 1. Фрагмент фазовой плоскости системы (1)

Источник: построен авторами по результатам исследования.

Вывод. Учитывая, что квадратичная система (1) может иметь только предельные циклы, окружающие единственную особую точку, которая является фокусом, а также не более двух фокусов в конечной части плоскости [19], заключаем, что рассматриваемая система циклов не имеет.

Анализ состояний равновесия на бесконечности. Построение схемы [1] (Bautin, Leontovich, 1990) полиномиальной автономной системы (1) подразумевает исследование состояний равновесия на бесконечности. Последнее проведем с помощью преобразования Пуанкаре.

Для определения характера возможных состояний равновесия применяется такое преобразование Пуанкаре [1] (Bautin, Leontovich, 1990): . Система (1) при этом переходит в систему 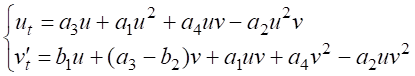(2):

. (2)

Приравнивая к нулю правые части, находим два состояния равновесия и 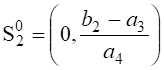, причем они сливаются, когда .

На основании теоремы Ляпунова об устойчивости по первому приближению заключаем, что в случае состояние является неустойчивым узлом, в случае будет седлом. Аналогично, в случае второе состояние 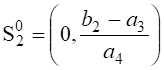будет седлом, а в случае оно будет неустойчивым узлом.

Отдельно рассматривается случай кратного состояния равновесия, когда . В этом случае систему (2) необходимо привести к каноническому виду и воспользоваться теоремой о кратном положении равновесия [1] (Bautin, Leontovich, 1990). Данное состояние оказывается неустойчивым седло-узлом.

Для определения характера возможных состояний равновесия применяется преобразование Пуанкаре [1] (Bautin, Leontovich, 1990) вида . Система (1) при этом переходит в систему 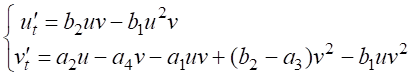(3):

. (3)

Приравнивая к нулю правые части, находим 2 состояния равновесия: и .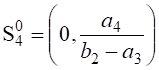

Вывод. Состояния равновесия и определяют и определяются одним и тем же состоянием равновесия на бесконечности автономной системы (1). Состояние равновесия является кратным. Тем же методом устанавливается, что оно будет устойчивым седлоузлом.

Полный бифуркационный анализ системы. Перейдем к полному описанию фазовых портретов системы (1). Напомним, что схемой называются сведения о характере состояний равновесия, предельных циклах и ходе сепаратрис фазового портрета автономной системы [1] (Bautin, Leontovich, 1990). Схема позволяет получить схематическое изображение всех фазовых портретов. Для системы (1) их оказывается 3 в зависимости от значений параметров и . Привлечение пакета Matlab+Simulink понадобилось для того, чтобы с помощью численных экспериментов понять, какие состояния связывают сепаратрисы. В результате было получено такое схематическое разбиение фазовых пространств на элементарные ячейки, являющиеся инвариантными множествами (рис. 2–4).

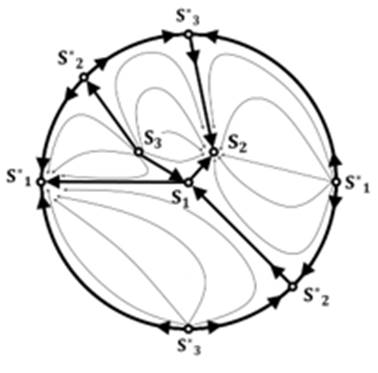
Рисунок 2. Фазовый портрет,

Источник: построен авторами по результатам исследования.

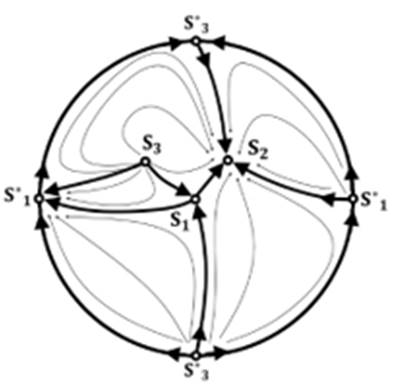
Рисунок 3. Фазовый портрет,

Источник: построен авторами по результатам исследования.

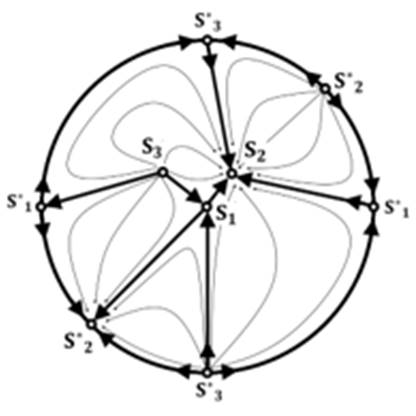
Рисунок 4. Фазовый портрет,

Источник: построен авторами по результатам исследования.

Вывод. Все траектории каждой такой ячейки асимптотически ведут себя одинаковым образом. Это знание позволяет качественно описать развитие во времени рассматриваемого экономического двумерного процесса по его начальному состоянию.

Построение синергетического регулятора системы (1). Синергетическое управление взаимосвязанными процессами спроса и предложения состоит в том [10] (Kolesnikov, 2006), чтобы заставить изменяться этот двумерный процесс по определенному закону, например, стабилизироваться в наперед заданном состоянии вне зависимости от начального его состояния. Это достигается с помощью аддитивного управления скоростью изменения какого-либо из этих процессов 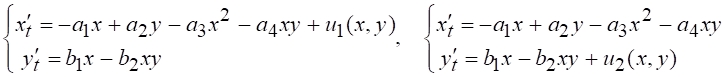(4):

(4)

Функция управления определяется функцией (агрегированной переменной) , задающей инвариантное множество проектируемой управляемой системой, называемой еще синергетическим регулятором. Это множество предполагается притягивающим в том смысле, что на траекториях проектируемого регулятора агрегированная переменная стремится к нулю. Поэтому состояния равновесия регулятора должны лежать на пересечении кривых и . То есть на выбор агрегированной переменной накладывается условие трансверсальности.

Пусть условие притягиваемости представлено в виде дифференциального уравнения с устойчивым состоянием равновесия (0,0), например, , где величина определяет скорость приближения к нулю [10] (Kolesnikov, 2006). Тогда дифференцируя это уравнение, получаем недостающее уравнение регулятора.

Так как требуемое состояние обязано лежать и на кривой, задаваемой неизменяемой правой частью исходной системы, то потенциальными терминальными состояниями могут быть только точки последней кривой. Это значит, что для решения поставленной задачи необходимо варьировать и параметры правой части a_i (или b_j) исходной системы. Нередко удается с помощью изменения одного или нескольких параметров покрыть графиками соответствующих кривых всю первую четверть (точки которой и имеют экономический смысл). Если при этом удается доказать, что любое терминальное состояние устойчиво, то можно считать, что задача синергетического управления системой решена.

Применим эти соображения к нашей системе.

Сначала будем управлять скоростью изменения x(t). Терминальные состояния должны лежать на кривой . Ограничиваясь ненулевыми состояниями, имеем горизонтальную полупрямую 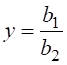в первой четверти. Нужно выбрать агрегированную переменную с параметром, чтобы при изменении последнего соответствующими кривыми пересекались все точки полупрямой, а также чтобы получаемые терминальные состояния регулятора были устойчивы [9] (Zubov, 1984). Простейшее семейство имеет вид . На траекториях проектируемого регулятора оно должно удовлетворять уравнению , где величина определяет скорость сближения траекторий регулятора с многообразием . Продифференцируем это выражение, заменим на и разрешим его относительно . Получим 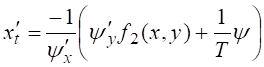. Объединяя это уравнение с первым уравнением системы (1), получаем такое уравнение регулятора:

.

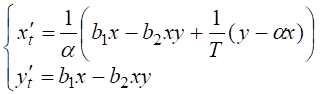Разрешая систему 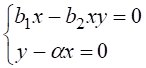, получаем следующее ненулевое состояние равновесия: 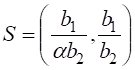. Очевидно, при пробегаются все точки полупрямой 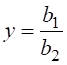из первой четверти.

Проверим условие устойчивости этого состояния [5, 9] (Bratishchev, 2017; Zubov, 1984).

.

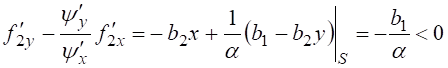Оно выполняется именно при .

Нами проведена верификация последнего результата с помощью проектирования S-модели регулятора (2) и построения при фазового портрета регулятора в окрестности его состояния равновесия. Видно (рис. 5), что все траектории фазового портрета стягиваются к терминальному состоянию (1,1).

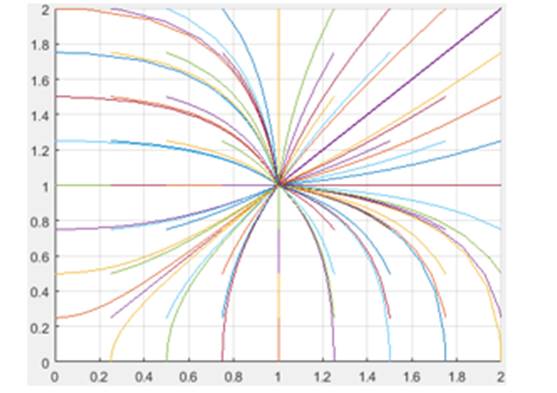
Рисунок 5. Фрагмент фазового портрета в окрестности терминального состояния

Источник: построен авторами по результатам исследования.

Замечание. Итак, любое допустимое терминальное состояние имеет вид

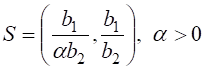. Поэтому, если мы хотим, чтобы наперед заданная точка первой четверти была терминальным состоянием регулятора с агрегированной переменной , надо сначала выбрать такими, чтобы 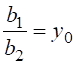, а затем выбрать параметр .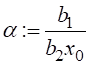

Найдем теперь аддитивное управление скоростью изменения переменной . График гиперболы подсказывает такой выбор агрегированной переменной: , так как семейство соответствующих кривых трансверсально этой кривой. Аналогичным образом получаем следующее уравнение регулятора:

.

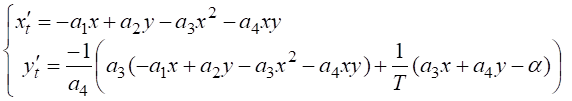Состояние равновесия последнего равно:

.

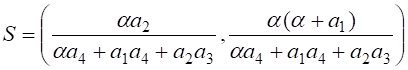Проверим условие устойчивости этого состояния:

.

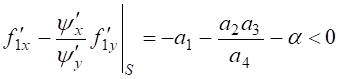Выводы. 1. Таким образом, терминальное состояние регулятора устойчиво при 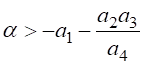. По экономическому смыслу нас интересуют значения . 2. Если мы хотим, чтобы наперед заданная точка первой четверти была терминальным состоянием регулятора, то сначала подбираем такие положительные значения параметров , чтобы выполнялось равенство . А затем образуем агрегированную переменную , где (или из предыдущего равенства следует

Устойчивость этого состояния проверяется также численным экспериментом.

Заключение. Проведенный численный эксперимент свидетельствует об устойчивости в целом состояния системы. Рассмотренная математическая модель динамической системы «Спрос и предложение» дает возможность строить прогнозы динамики взаимосвязи спроса и предложения при любых заданных начальных состояниях системы с целью достижения динамического равновесия.