Математическая постановка задачи минимизации потерь фирмы, оказывающей интеллектуально-креативные услуги

Интеллектуально-креативные ресурсы, как важнейший фактор повышения эффективности в любой сфере деятельности в большинстве случаев сохраняют и даже увеличивают степень своей эффективности по мере утверждения и развития постиндустриальной экономики. Поэтому возникает объективная задача оптимального распределения этих дефицитных ресурсов для получения максимального эффекта их использования при решении наиболее сложных и актуальных задач.

В настоящее время ресурс времени креативных работников распределяется руководителями фирмы интуитивно, исходя их собственного опыта и принципа максимума ожидаемых выгод при минимуме ожидаемых неприятностей, что в большинстве случаев не поддается формализации. Такие ситуации возникают при дефиците высококвалифицированных рабочих, управленческих кадров, адвокатов, следователей, врачей, научных работников, педагогов и пр., когда потребность в услугах этих креативных служащих превышает их временной ресурс.

В зависимости от различных вариантов такого распределения возникают неодинаковые потери от дефицита этих ресурсов, которые вследствие сложности задачи и отсутствия необходимой информации не учитываются. Между тем, они могут быть довольно значительными, поэтому возникает необходимость минимизировать эти потери при распределении времени креативных работников между различными объектами применения этих услуг.

Математическая постановка задачи минимизации потери любой фирмы, оказывающей интеллектуально-креативные услуги.

Предполагается, что распределение имеющегося у фирмы интеллектуально-креативного ресурса , меньшего потребности в нем, можно заменить распределением отклонения 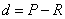. Указанное отклонение условно названо дефицитом. Предположим, что есть объектов, которые пользуются этими услугами и которым руководство при распределении ограниченного ресурса автоматически устанавливает меру дефицитности . Издержки дефицитности являются функциями дефицита и равняются соответственно . Предположим, что неотрицательны и возрастают с увеличением , т.е. назовем предельными издержками дефицитности. Допустим, что и возрастает c увеличением , т.е. . Это равносильно предположению, что стоимостная функция издержек задана в классе выпуклых функций, т.е. цена дефицита растет с увеличением размера дефицита.

Задача заключается в таком распределении между клиентами, чтобы суммарные издержки дефицитности были минимальными. Математическая постановка задачи такова: найти такие значения переменных , чтобы (1),

при соблюдении следующих побочных условий:

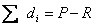(2)

и при граничных условиях .

С математической точки зрения речь идет об определении экстремума функции многих переменных, который будем искать методами дифференциального программирования. Ищем вспомогательную функцию Лагранжа в виде:

,

, если и, следовательно, распределение дефицита оптимально, если предельные издержки дефицитности у всех потребителей равны между собой. Всего будет таких уравнений, из которых определяется неизвестных . Последнее определяется из балансового уравнения (2).

Это же условие можно вывести логическим путем. Если бы предельные издержки дефицитности у отдельных потребителей услуг не были равны, то было бы выгодно перераспределить дефицит, переместив его частично от потребителей услуг с высокими предельными издержками к потребителям услуг с более низкими предельными издержками. Это привело бы к снижению суммарных издержек от дефицитности. Если у всех потребителей услуг предельные издержки дефицитности одинаковы, то можно говорить об общих предельных издержках по всей управленческой структуре. Они равняются . В этом заключается экономический смысл множителей Лагранжа.

Если распределение не оптимально, то предельные издержки у различных потребителей услуг не одинаковы, и в этом случае нельзя говорить о таких-то общих для всех потребителей предельных издержках, которые будут неодинаковы у потребителей услуг. Таким образом, если при распределении дефицита не имеет места проблема риска, то оптимальное распределение ресурса (р) по отдельным потребителям услуг должно быть таким, чтобы предельные издержки у всех потребителей услуг были одинаковы.

В действительности фактический дефицит под воздействием различных случайных причин может отличаться от ожидаемого дефицита . Обозначим через так назы­ваемый коэффициент неопределенности, на который следует умножить ожидаемого дефицит, чтобы получить фактический дефицит. Коэффициент есть случайная величина, которая принимает различные значения с определенной вероятностью или с определенной плотностью вероятности. Для упрощения будем считать коэффициенты неопределенности непрерывными случайными переменными, т.е. принимать, что для каждого существует определенная и известная функция плотности вероятности. В частном случае она может характеризоваться нормальным законом распределения, когда математическое ожидание фактического дефицита у -го потребителя равно плановому

. (3)

Пусть дисперсия возможного отклонения фактического дефицита от ожидаемого

не должна превышать заранее определенной величины

. (4)

Математическая формулировка задачи – найти такие неотрицательные , чтобы суммарные издержки дефицитности были минимальны, т.е.

, (5)

где – удельные издержки, связанные с получением единицы дефицитного продукта, например путем аутсорсинга.

Побочные условия

, (6)

. (7)

Функция Лагранжа:

(8)

(9)

(10)

Выражение (9) получено дифференцированием (8) по уравнения (10), число которых равняется , и дополнительные условия (6) и (7) определяют переменных 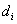, а также и . – разность между предельными издержками и удельными издержками можно назвать чистыми предельными издержками. В случае отсутствия проблемы риска чистые предельные издержки равны . При наличии риска чистые предельные издержки уменьшаются на величину . Побочные условия (7) означают, что дисперсия отклонения фактического дефицита от ожидаемого не должно превосходить заранее фиксированной величины , являющейся пределом риска, на который можно пойти при распределении дефицита.

В терминах неоклассической тории риска данную задачу можно сформулировать следующим образом. Необходимо так распределить ожидаемые дефициты между отдельными потребителями, чтобы суммарные издержки дефицитности были минимальны:

, причем должны выполняться следующие балансовые условия:

, (12)

. (13)

Зависимость (13) означает, что вероятность появления дефицита, а следовательно, и вероятность возникновения непредвиденных хозяйственных трудностей не должна превышать некоторой заранее установленной величины 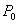, которую можно назвать коэффициентом риска.

Решая данную задачу, как и ранее, методом множителей Лагранжа:

. (14)

Вычисляя частные производственные функциии приравнивая их к нулю, имеем, что

(15)

или

. (16)

Условие (16) означает, что распределение ожидаемого дефицита оптимально, если разность между предельными издержками и произведением для каждого потребителя одинакова. Если отбросить условие (12), по которому общий фактический дефицит не может превышать общий внутриплановый дефицит и, следовательно, принять , то получим следующее условие оптимальности распределения дефицита:

,

(17)

Условие (17) можно записать в виде

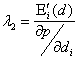
, (18)

откуда следует, что распределение оптимально, если предельные издержки дефицитности, приходящиеся на единицу вероятности возникновения дефицита, для всех потребителей услуг одинаковы. Это как бы «цена», которую мы готовы заплатить за уменьшение на единицу вероятности возникновения дефицита. Иными словами, – это коэффициент взаимозаменяемости между предельными издержками дефицитности и вероятностью возникновения дефицита. Данное рассмотрение предполагает, что функция вероятности возникновения дефицита известна.

Однако рациональная интеллектуальная составляющая сохраняется при оценке специалистов креативного класса и их поиске, при формировании мотивационных механизмов для продуцентов интеллектуально-креативных услуг и производственных коллективов на рынке этих услуг, а также при оценке их эффективности.