Анализ динамики цены спот нефти марки WTI за период 1994-2016 гг.

Введение

В данной статье приведены результаты исследования баланса спроса и предложения на динамику нефти за период с 2008 по 2016 год. Построена сырьевая модель ценообразования на основании интегральных оценок спроса и предложения и дифференциальных оценок нефтяных запасов развитых стран.

Breitenfellner и Cuaresma (2008) и МВФ (2008) анализировали связь между курсом доллара США и ценами на нефть. Во-первых, поскольку цена на нефть выражена в долларах, то и обесценение доллара может повысить спрос на нефть в «недолларовых» странах, т.к. нефть, выраженная в долларах, становится менее дорогой. Во-вторых, цена на нефть. Более дешевый доллар уменьшает доходы производителей нерезидентов США, что вынуждает их наращивать добычу и повышает предложение. В-третьих, обесценение доллара снижает доход номинированных в долларах финансовых активов, что делает более привлекательными вложения в сырьевые товары (такие как нефть) для иностранных инвесторов. К тому же сырье может стать более привлекательным для американских инвесторов в виде хеджирования инфляции, если обесценение доллара будет подогревать инфляционные ожидания. В-четвертых, падение курса доллара может привести к экспансионистской денежной политике вне США, особенно в странах, валюты которых привязаны к доллару. Низкие процентные ставки и увеличение предложения денег может увеличить спрос на нефть.

Исследования Akram (2009) и Krichene (2006, 2008) показали, что изменения курса американского доллара оказывает существенное влияние на нефтяные цены, в частности, негативные долларовые шоки оказывают положительное влияние на динамику нефти. Подобного мнения придерживаются и аналитики (Diwan (2008), Deutsche Bank (2008, 2009)).

Исследование МВФ (2008) использует приведенную модель ценообразования, основанную на обменном курсе доллара США, объем мирового промышленного производства, ставку федеральных фондов (federal funds rate) и запасы ОЭСР. Выяснилось, что номинальный эффективный валютный курс оказывает значительное воздействие на номинальные нефтяные цены, как в краткосрочной, так и в долгосрочной перспективе. В долгосрочной перспективе (от 12 до 24 месяцев) уменьшение номинального курса доллара на 1% влечет увеличение номинальной стоимости нефти примерно на 1%. Влияние реального эффективного обменного курса оказывает еще большее влияние на реальные цены в долгосрочной перспективе. Согласно исследованию, если курс доллара останется неизменным на период с 2002 (максимальные значения) по 2007 гг., то номинальные нефтяные цены упадут примерно на 25 долл. к концу 2007 года.

Однако данные исследования были проведены в 2008 году, еще до того, как ставка fed funds упала до околонулевых значений. Ставка оставалась таковой вплоть до декабря 2015 года, и, в отсутствие вариации, эта переменная плохо объясняет движения курса.

Сырьевая модель ценообразования

Спрос и предложение

При определении модели ценообразования актива первым образом естественно встает вопрос о балансе спроса и предложения. Подразумевая это, построена линейная однофакторная регрессия, где в качестве независимой переменной мы взяли разность мирового потребления и мирового спроса. Однако модель оказалась крайне низкого качества. Коэффициент детерминации оказался равен 0.18, что говорит о том, что связи нет.

Тем не менее здравый смысл и элементарные законы экономики подсказывали нам, что истина кроется именно в этом направлении. Тогда было решено взять не моментальную разность потребления и производства, а скользящее среднее разности потребления и производства. Оставался открытым вопрос о том, какое следует использовать окно усреднения и каков будет лаг модели.

Были проанализированы лаги от T-6 (т.е., грубо говоря, июньская цена на нефть объясняется январской разностью потребления и производства) до T+0.

Ниже представлены результаты 312 однофакторных регрессий. В качестве зависимой переменной выступало среднемесячное значение спот-цены нефти марки WTI, в качестве независимой переменной – разность мирового потребления и спроса по данным Energy Information Administration (независимое агентство в составе федеральной статистической системы США, ответственное за сбор, анализ и распространение информации об энергии и энергетике). Значения таблицы – нормированные коэффициенты детерминации каждой регрессии.

По результату эксперимента можно заключить следующее:

1. Наибольшая доля объясненной дисперсии соответствует моделям вида .

2. Из моделей вида наибольшим качеством обладают те, в которых использовались окна усреднения в 10, 11 и 12 месяцев.

3. Максимальное значение коэффициента детерминации в 0.755 говорит о высоком качестве модели и наличии существенной связи между регрессором и регрессантом.

4. При прогнозировании требуется большее окно усреднения.

5. Для прогнозирования на 1 месяц вперед, т.е. модель вида требуется использовать окно усреднения в 12 месяцев, иными словами, будущую цену определяет среднегодовая разность спроса и предложения.

Запасы

Очевидно, что на определение стоимости сырья влияет не только баланс спроса и предложения, но и запасы. Ниже на рисунке представлены реальные значения нефти марки WTI и линейной регрессии, где в качестве независимой переменной выступает величина запасов сырой нефти в странах ОЭСР. Коэффициент детерминации равен 0.61 и уравнение имеет вид:

Однако в случае с запасами использование скользящего среднего не приносит никакой пользы. В таблице результаты регрессий для различных окон усреднения и различных лагов. Очевидно, что с целью улучшения модели надо двигаться в другом направлении.

По построенной коррелограмме ряда независимой переменной (запасы) четко видно, что коэффициент авторегрессии убывает вплоть до лага +13.

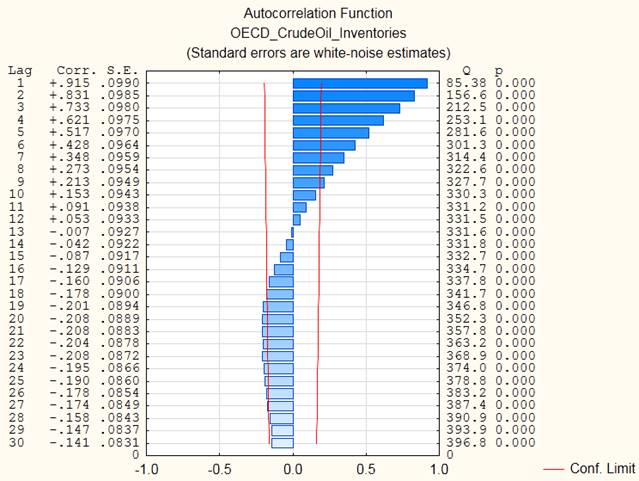
Мы получили подтверждение того, что включать среднюю величину запасов в модель бессмысленно. Кроме того, получается, что память процесса угасает вплоть до 13 лага, имея с ним наименьшую корреляцию.

Вышеизложенное, а также предположение, что динамику цены определяют не столько сами запасы, а их изменение, привело к следующей задаче оптимизации. Мы будем исследовать, с одной стороны, изменение запасов за тот период, какой лучшим образом объясняют динамику нефти. С другой стороны, мы рассмотрим вопрос лагов.

Под изменением запасов мы будем подразумевать разность показателя текущего месяца и базового. Таким образом, для расчета показателей разности за июнь М-1 означает разность июньских и майских данных, а М-5 – разность июньских и январских.

Ниже представлен результат 312 однофакторных регрессий.

На его основе можно заключить следующее:

1. Максимальное значение коэффициента детерминации составляет 0.7292 и имеет быть при лаге Т-1 и разности порядка М-11. Таким образом, здесь мы получили результат, схожий со спросом/потреблением, где наиболее существенным оказалось скользящее среднее с периодом 11.

Кроме того, само значение коэффициента достаточно высоко, чтобы говорить о наличии существенной связи.

2. Крайне любопытным является факт наличия двух локальных максимумов.

Таким образом, в модель рационально включить разности М-11 с лагом T-1 и М22 с нулевым лагом.

Добыча «сланцевой» [1] нефти

Следующий показатель, достойный рассмотрения, – динамика добычи сланцевой нефти. К сожалению, данных, касающихся количества именно установок, добывающих нефть методом гидроразрыва пласта, в открытом доступе не удалось найти. Однако о них можно судить по косвенным данным. В США около 80 % [2] установок занимаются добычей так называемой «сланцевой» нефти. Таким образом, рост добычи сланцевой нефти в подавляющей степени обусловлен ростом числа добывающих установок. Связано ли число этих самых установок с ценой на нефть, и если да, то какая связь?

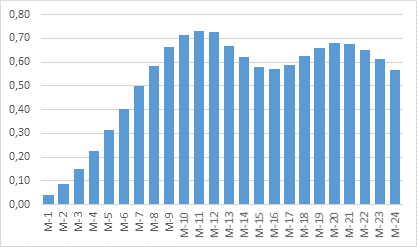
Ниже приведена динамика коэффициента детерминации для различных лагов

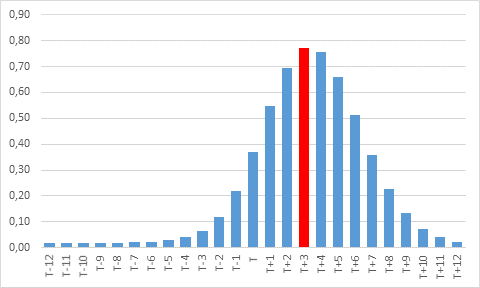
Видно, что максимальный уровень достигается при лаге T+3. Получается, что цена на нефть определяет количество добывающих установок (уровень добычи сланцевой нефти), а не наоборот. При нулевом лаге коэффициент детерминации составляет меньше , что говорит о крайне слабой связи.

Полученный результат хорошо соотносится с тем фактом, что время, затрачиваемое на разработку скважины по добыче «сланцевой» нефти, составляет как раз три месяца.

Финансовая составляющая

Двухфакторная модель достаточно хорошо описывает динамику нефти, однако ее можно существенно улучшить.

Ниже представлены коэффициенты детерминации для трехфакторных моделей, где в качестве первых двух факторов взяты переменные, описанные в предыдущих пунктах, а в качестве третьего – исследуемая финансовая переменная:

· Индекс доллара (за уровень в 100 взято значение 2010 года).

· Чистая инвестиционная позиция США.

· Инвестиционный доход США.

· Объем количественного смягчения Федеральной резервной системы США, а именно:

o Объем поддержки краткосрочной ликвидности финансовых институтов.

o Объем поддержания ликвидности на рынках кредитования (выкуп бумаг mutual funds, а также о выкупе ААА CDO, состоящих из кредитов на обучение, автокредитов и кредитных карт).

o Стандартная (базовая) величина активов ФРС.

o Объем программы выкупа ипотечных ценных бумаг.

Модель

Окончательная модель имеет вид:

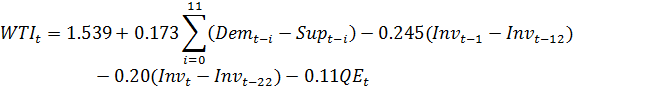
– среднемесячная спот-цена нефти марки WTI;

– мировое потребление нефти;

– мировое производство нефти;

– запасы нефти в странах ОЭСР;

– объем количественного смягчения ФРС;

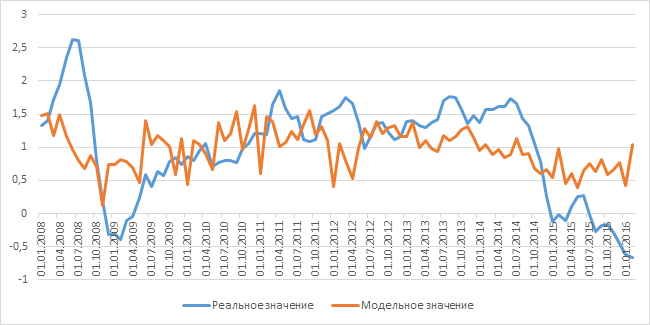
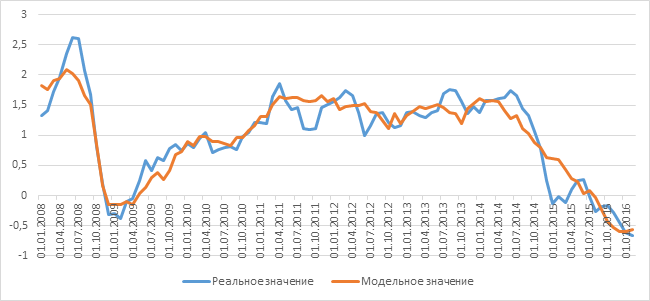
Коэффициент детерминации модели равен 0.873, ниже представлено модельное и наблюдаемое значение:

Заключение

В работе было показано существенное влияние сырьевых факторов, таких как спрос, предложение и запасы на динамику стоимости нефти марки WTI. Дан количественный анализ вклада каждого из факторов. Было показано, что цена на нефть действительно сильно связана с сырьевыми факторами, несмотря на тот факт, что большинство исполняемых фьючерсных контрактов на нефть являются беспоставочными и носят спекулятивный характер. Кроме того, было выяснено, что динамика добычи так называемой сланцевой нефти является следствием нефтяных цен.

В заключение была дана оценка вклада финансовых показателей на динамику нефтяных цен. Была открыта высокая степень корреляции цен на нефть с чистой инвестиционной позицией и инвестиционным доходом США. Тем не менее, так как цена нефть определяется в первую очередь спросом и предложением, данные переменные не показали существенного влияния в модели.

[1] Под «сланцевой нефтью» подразумевается так называемая tight oil (также shale oil, light tight oil, LTO). Данная нефть характеризуется тем, что её добыча требует применения многостадийного гидроразрыва пласта и точного наклонно-направленного бурения с протяжёнными горизонтальными участками.

[2] По данным Baker Hughes (http://www.emirates247.com/news/crude-oil-prices-above-46-as-us-shale-rig-count-slumps-80-2016-04-21-1.627976)