Панельные данные в анализе регионального агропромышленного комплекса

Введение

Развитие инструментария анализа динамических данных неразрывно связано с развитием технических средств, применяемых в процессе этого анализа. В частности, качественный скачок произошел в 80-е годы 20 века, когда с появлением ЭВМ стала возможной обработка больших массивов информации, а именно панельных данных.

Под панельными данными понимается пространственно-временной массив информации, в котором пространственная часть представляет собой статическую причинно-следственную взаимосвязь экономических переменных. При этом желательно, чтобы одна из экзогенных переменных имела географическую привязку (например, сравнение эндогенной переменной по странам, городам, различным предприятиям и пр.). Временная часть панельного массива – это изменение всех рассматриваемых переменных во времени [1].

Следует отметить, что при формировании панельных данных к пространственной части применяются все требования, предъявляемые к пространственной информации, в частности, отсутствие мультиколлениарности между переменными; к временной части – требования, предъявляемые к динамическим рядам, в частности, требование сопоставимости рядов [2].

Сегодня панельные данные являются хорошим инструментом анализа экономической информации, и существует достаточно много работ, посвященных применению данного инструмента в анализе и прогнозировании различных экономических процессов.

Например, большая группа работ показывает целесообразность использования инструментария анализа панельных данных при оценке различного вида экономических рисков. Так, в работе Тростянского С.Н. оценивается вероятность возникновения пожаров в регионах России [3]; в работе Полякова К.Л. оценивается вероятность риска банкротства коммерческих банков [4]; в работе Сиротина В.П. оцениваются политические риски в моделях инвестирования развивающихся экономик [5].

Другая группа работ посвящена изучению возможностей применения панельных данных в оценке деятельности промышленных предприятий. Например, в работе Бахитовой Р.Х. проводится классификация регионов России по схожести производственных функций, лежащих в основе оценки объема выпускаемой ими продукции [6]. В работе Авдейчик О.В. проводится оценка инновационной деятельности промышленных предприятий [7].

Достаточно часто инструментарий анализа панельных данных применяется в анализе секторов и отраслей российской экономики: нефтяного сектора [8], лесопромышленного сектора [9], туристической отрасли [10].

Применение методов панельных данных в анализе зависимости численности сельского населения муниципальных образований Ленинградской области от уровня развития сельского хозяйства рассматривается в работе Никулиной Ю. Н. [11]. Оценка выпуска продукции животноводства регионов Нечерноземной зоны России на валовой выпуск региона с помощью эконометрических моделей панельных данных с фиксированными и случайными эффектами нашло отражение в работе Юрченко Т.В. [12].

Актуальность настоящего исследования обусловлена оценкой агропромышленной отрасли РФ, в частности, региональный аспект эффективности государственных инвестиций, активно поступающих в данный сегмент экономики, начиная с 2014 года, с момента введения ограничительных санкций на АПК России и принятия Правительством РФ Доктрины продовольственной безопасности РФ [13], используя инструментарий анализа панельных данных, чего ранее не было сделано.

Авторская гипотеза состоит в предположении того, что регионы РФ обладают индивидуальными особенностями, которые невозможно описать количественными переменными и использовать для их оценки классические методы анализа временных рядов или модели регрессии. Использование панельных данных даст возможность получить оценку специфических характеристик рассматриваемых АПК регионов страны.

В качестве объекта исследования выступает сектор АПК всех восьми федеральных округов РФ. В качестве переменных, описывающих динамику развития АПК каждого региона были рассмотрены: у – продукция сельского хозяйства, млрд.руб., х1 – посевные площади сельскохозяйственных культур, млн.га, х2 – число предприятий и организаций в АПК, тыс.шт., х3 – инвестиции в основной капитал в сфере АПК, млрд.руб., х4 – ввод основных фондов в сфере АПК, млрд.руб. В качестве временного интервала исследования был рассмотрен период с 2012 по 2023 год [14].

Материалы и методы

Использование инструментов анализа панельных данных с целью выявления скрытых тенденций, основывается на сравнении трех моделей: модели пула, модели с фиксированным эффектом и модели со случайным эффектом [15].

На первом шаге моделирования построим модель пула (Pool model) – регрессию по объединенной выборке, предполагая отсутствие неоднородности между пространственными объектами: , .

Применяя обычный МНК-метод, получаем уравнение:

.

Коэффициент детерминации полученной модели равен и он значим по критерию Фишера. Параметры данной регрессии являются несмещенными и эффективными оценками, а при или являются и состоятельными оценками коэффициента b регрессии. Таким образом, их значимость может быть проверена с помощью критерия Стьюдента: .

Далее построим модель регрессии с фиксированным эффектом (FE):

, где параметр принимает различные значения для каждого экономического объекта выборки. Его смысл в том, чтобы отразить влияние ненаблюдаемых переменных, характеризующих индивидуальные особенности исследуемых объектов, в нашем случае – субъектов РФ, не меняющихся во времени. Значения параметра могут отличаться между объектами, но для каждого конкретного объекта он не меняется с течением времени t.

Для построения данной регрессии использует метод корректировки на индивидуальные средние: , где , , [15].

Используя МНК-метод, в нашем случае получаем уравнение:

, где и он значим. Полученные оценки, которые также называются внутригрупповые, состоятельны только при и .

Фиксированные эффекты находятся с помощью равенства: , , которые являются несмещенными и состоятельными для фиксированного n при .

Таким образом, в нашем случае, влияние ненаблюдаемых переменных, характеризующих индивидуальные особенности субъектов РФ, представлены в таблице.

Таблица - Индивидуальный эффект влияния факторов на продукцию сельского хозяйства по субъектам РФ модели с фиксированными эффектами

Полученные значения говорят о том, что например для ПФО, факторы, которые присущи данному региону (например, географическое положение, инфраструктура, управленческий менеджмент и пр.) снижают посевные площади, увеличивают количество предприятий АПК, привлекают дополнительные инвестиции в АПК и увеличивают ввод основных фондов. Все это говорит о том, что ПФО является аграрным регионом, позволяющим при меньших площадях получать более высокие показатели работы АПК.

На следующем этапе анализа построим модель со случайным эффектом (RE): , где – ошибка модели, в которой слагаемое – случайные эффекты, отражающие наличие у субъектов исследования некоторых индивидуальных характеристик, не изменяющихся со временем, которые трудно наблюдать или измерить. И поскольку ошибка классической регрессионной модели возникает за счет невозможности включения в модель всех объясняющих переменных, то такие индивидуальные эффекты включаются в общую погрешность модели. Здесь .

Для построения модели со случайным эффектом используется следующий алгоритм [16]:

1. находим и по полученным значениям строим регрессию: ;

2. по полученной регрессии находим остаточную дисперсию ;

3. находим – остаточную дисперсию из модели с фиксированными эффектами: ;

4. находим ;

5. находим веса и ;

6. переходим к новым переменным: и и строим по ним регрессию: .

В последней регрессии и он значим, параметры модели, называемые также межгрупповыми параметрами, являются несмещенными.

Алгоритм, применяемый для построения модели со случайным эффектом, основывается на обобщенном МНК-методе и дает модель, которая является средневзвешенным между межгрупповой оценкой, учитывающей только межгрупповую изменчивость, и внутригрупповой оценкой, учитывающей только внутригрупповую изменчивость, весами же являются коэффициенты , показывающие межгрупповую изменчивость.

Результаты

Выше было построено три модели регрессии: модель пула, которая строилась по общей выборке и не учитывала никакие индивидуальные характеристики экономических объектов; модель с фиксированным эффектом, в которой предполагается наличие неизменных во времени индивидуальных характеристик для каждого экономического объекта исследования; модель со случайным эффектом, в которой индивидуальные характеристики являются случайными величинами.

Таким образом, возникает задача оценки качества полученных регрессий и выбора лучшей модели.

В обычном регрессионном анализе в качестве меры оценки полученного уравнения регрессии используется коэффициент детерминации , показывающий долю объясненной вариации зависимой переменной. В моделях с панельными данными понятие коэффициента детерминации требует уточнения, поскольку внутригрупповая и межгрупповая регрессии имеют дело с разными вариациями зависимой переменной, а также, поскольку используется обобщенный, а не обычный МНК-метод.

Основываясь на том, что коэффициент детерминации равен квадрату коэффициента корреляции между и прогнозным значением , положим [17]:

- для внутригрупповой регрессии (т.е. модели с фиксированным эффектом) , где – квадрат выборочного коэффициента корреляции; ; объем выборки равен nT;

- для межгрупповой регрессии , где ;

- для обычной модели коэффициент объединенной детерминации , где .

В нашем случае: ; ; .

С целью выбора лучшей модели используется ряд тестов [18]:

- для сравнения модели пула с моделью с фиксированным эффектом: выдвигается гипотеза , что соответствует модели с одним и тем же параметром a для всех объектов наблюдения (модель пула) против альтернативной гипотезы (модель с фиксированным эффектом); тестовая статистика , где – коэффициент множественной корреляции модели с фиксированными эффектами, – коэффициент множественной корреляции модели пула; если следует выбрать модель пула, в противном случае – модель с фиксированным эффектом;

- для сравнения модели пула с моделью со случайным эффектом используется тест Бройша-Пагана: выдвигается гипотеза (модель пула); статистика критерия 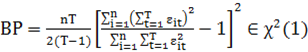, где остатки берутся из модели пула; если , то следует выбрать модель пула, в противном случае – модель со случайным эффектом;

- для сравнения модели со случайными эффектами с моделью с фиксированными эффектами используется тест Хаусмана: ; ; статистика , где – оценка матрицы ковариаций ; если , то следует выбрать модель со случайным эффектом, в противном случае – модель с фиксированным эффектом.

В нашем случае, в первом тесте , поэтому гипотеза Н₀ отклоняется и необходимо выбрать модель с фиксированным эффектом. Во втором тесте , следовательно гипотеза Н₀ отклоняется и необходимо выбрать модель со случайным эффектом. В третьем тесте , поэтому гипотеза Н₀ отклоняется и необходимо выбрать модель с фиксированным эффектом.

В результате можно сделать следующие выводы. Во-первых, в процессе формирования продукции сельского хозяйства по регионам РФ присутствуют индивидуальные эффекты, которые обусловлены факторами, характерными для каждого отдельного региона РФ. Во-вторых, данные индивидуальные эффекты носят фиксированный характер, что подтверждается тестом Вальда и тестом Хаусмана, т.е. факторы, определяющие производство сельхозпродукции в каждом регионе свои и они не меняются там во времени. В-третьих, несмотря на то, что качество полученной модели со случайным эффектом выше (больше , параметры более статистически значимы, что следует из более высокой состоятельности оценок RE-модели), дополнительные тесты показывают ее необоснованность в качестве модели аппроксимации.

Заключение

Рассмотренный в работе пример использования инструментов анализа панельных данных к исследованию регионального АПК, показал их возможности в оценке скрытых зависимостей и выявлении факторов, не участвующих в исследовании явным образом.

Полученный в работе результат – наличие фиксированных индивидуальных эффектов в АПК-деятельности экономических объектов – согласуется с тем фактом, что модели с фиксированными эффектами обычно используются в ситуациях, когда экономические объекты нельзя рассматривать как случайную выборку из некоторой более широкой совокупности (популяции). В нашем случае – федеральные округа, рассмотренные в работе, представляют собой всю генеральную совокупность.

Модели со случайными эффектами используются тогда, когда исследователя интересуют не конкретные экономические объекты, а обезличенные образы, имеющие заданные характеристики.