Sistemnye riski na finansovyh rynkakh

1. Введение

Анализ причин и последствий финансового кризиса 2007-2009 гг. выделил вопрос о системных финансовых рисках как один из наиболее значимых. На фундаментальном уровне понятие системных рисков возникает при анализе смены режимов в сложных адаптивных системах, к которым, несомненно, относится и финансовый̆ рынок. Интуитивно системный риск связывается с эффектами взаимодействия экономических агентов, приводящим к значимым последствиям для системы в целом. Дать точное компактное определение системного риска, по-видимому, невозможно, и наиболее полное его описание представляет собой̆ подробное перечисление сценариев, которые можно классифицировать как относящиеся к системным рискам, см. напр. [1]. Количественный̆ анализ системных рисков находится в центре внимания Банка России [2, 3], международных организаций (МВФ) [4, 5, 6, 7] и академической̆ науки [9, 10, 11].

2. Межбанковская сеть как ориентированный взвешенный граф

Исходной точкой для количественного анализа системных рисков на межбанковском рынке является его представление в виде взвешенного ориентированного графа, в узлах которого находятся банки, а на ребрах – обязательства банков по отношению к друг другу. Направленность ребер условна, но чаще всего используется соглашение, по которому ребро направлено от должника к кредитору. Таким образом, в матрице W, характеризующей рассматриваемый граф

займу, выданному банком j банку i, отвечает ребро с направлением i ‑> j. В этих обозначениях чистым заемщикам отвечают узлы, у которых есть только выходящие (out-) ребра, чистым кредиторам – узлы, у которых есть только входящие (in-) ребра и, наконец, банкам, являющимся одновременно кредиторами и заемщиками, отвечают узлы, у которых есть как входящие, так и выходящие связи. Во всех случаях значения матричных элементов равны величине соответствующих займов. Описанная классификация узлов отвечает так называемой bow-tie декомпозиции ориентированного графа на три основные компоненты Out -> In-Out -> In. На рис.1 показана bow-tie структура для рынка межбанковского кредитования РФ:

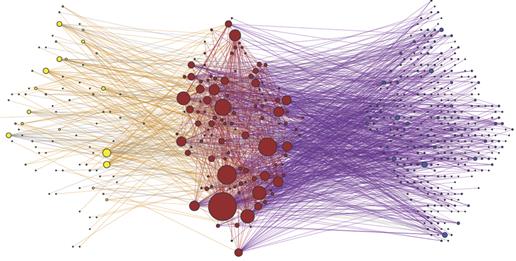
Рис. 1. Компонентная структура рынка МБК РФ [14]

Количественный анализ компонентной структуры рынка МБК РФ, проведенный в работе [12], показал, что большинство банков (порядка 60 %) являются чистыми кредиторами. Вместе с тем, как видно из рис. 1, абсолютное большинство крупных банков принадлежит к In-Out ядру.

3. Каскадный дефолт: модель Гая-Кападии [12]

Построение современных количественных моделей каскадного дефолта на рынке межбанковского кредитования во многом следует пионерской работе [12]. Рассмотренная в [12] механика распространения каскадного заражения выглядит следующим образом. Рассмотрим узел сети (банк) с индексом i, у которого имеется k входящих и j выходящих ребер, т.е. k банков – должников и j банков – кредиторов, где каждое ребро “нагружено” величиной соответствующего займа. Рассмотрим простейший случай и предположим банкротство одного из k заемщиков банка i. Распространение дефолта имеет место в том случае, когда результатом исходного дефолта является дефолт банка i, т.е. когда для узла i в результате невозврата долга обанкротившимся должником нарушается институционально установленный баланс пассивов и активов. В балансе банков учитываются активы A, в том числе относящиеся к рынку МБК активы A^IB и пассивы L. Тем самым, достаточность капитала K_i для узла i равна K_i=A_i-L_i. В модели [12] используется простейшее предположение о равномерном распределении активов A^IB_, относящихся к межбанковским кредитам, по входящим в узел ребрам. В этих предположениях дефолт одного из контрагентов приводит к дефолту рассматриваемого узла, если

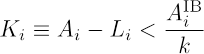
Ключевым шагом в формулировке математической модели каскадного дефолта является переход к вероятностному описанию, основанном на введению вероятности v_k дефолта узла степени k при дефолте по одной из ходящих в этот узел связей

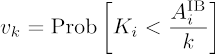
и описании межбанковского рынка кредитования как древесного ориентированного графа с распределением вероятностей по числу входящих и выходящих ребер p_ik. В рассматриваемой формулировке задача сводится к стандартной задаче о перколяции ребер на ориентированном графе. Основной фокус анализа системных рисков на рынке МБК в работе [12] был сделан на вопросе о возможности появлении гигантского перколяционного кластера и связанным с этим обрушения рынка в целом.

4. Системные риски на межбанковском рынке РФ [13, 14]

Существенный интерес представляет обобщение результатов работы [12] и выработки модели каскадного дефолта, учитывающего как реалистическую топологию взвешенного графа рынка МБК, так и реалистические балансы банков. Такая модель был построена для рынка МБК России в работах [13,14].

Указанных данных в принципе достаточно для изучения рисков, связанных с возможными каскадными дефолтами путем численных симуляций. Возможность аналитического описания связана, однако, с тем, насколько сложной является типичная топология дефолтных кластеров. Численные исследования [13,14] выявили следующие характерные особенности каскадных дефолтов:

· Условные вероятности распространения дефолта зависят от функциональной роли (положения относительно bow-tie структуры графа МБК) как узла – триггера, так и узла – реципиента дефолтного шока.

· Несмотря на то, что топология исходного графа существенно отличается от древесной и, в частности, характеризуется высокой степенью кластеризации, в подавляющем большинстве случаев дефолтные кластеры являются древесными.

· Изучаемый каскадный процесс характеризуется существенной зависимостью от вероятностной взаимосвязи между степенями соседних узлов, которая для всех изученных банковских сетей отвечает наличию выраженной дисассортативности, когда соседом узла с большим числом ребер является узел с малым числом ребер, и наоборот.

Эффективная древесность дефолтных кластеров позволяют построить модель распространения каскадного дефолта, использующую хорошо разработанный формализм производящих функций и учитывающего как дисассортативность сети МБК, так и зависимость вероятности распространения дефолта от узла-донора к узлу-реципиенту [13,14]. Сравнение предсказаний модели с результатами численной симуляции для распределения по размеру дефолтных кластеров приведено на рис. 2.

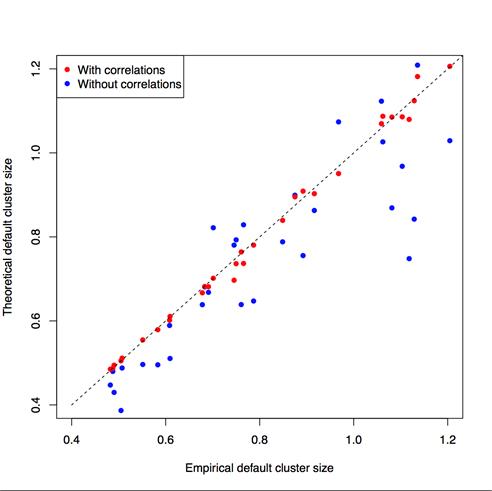
Рис. 2. Эмпирическое распределение по размерам дефолтных кластеров (пунктир) в сравнении с предсказаниями теории без учета (синий) и с учетом (красный) корреляций степеней соседних узлов (дисассортативности) сети МБК [14]

Из рис. 2 мы видим, что учет дисассортативности критически важен для реалистического описания процесса каскадного дефолта.

Как уже упоминалось выше, основным типом системных рисков на рынке МБК, изучавшимся в пионерской работе [12] и ряде последующих публикаций, являлся риск возникновения гигантской дефолтной компоненты., т.е. в режиме перколяции В то же время, методология формализма, использованного в работах [12,13,14] позволяет оценить, находится ли реальная сеть МБК в перколяционном режиме. Подробный анализ [14] показал, что сеть МБК России всегда находилась весьма далеко от точки перколяции и, в этом смысле, является устойчивой по отношению к системному риску, рассмотренному в работе [12].

5. Заключение

В заключение сформулируем еще раз наши выводы:

· Рассмотрение каскадных дефолтов на рынке МБК является важной составляющей анализа системных рисков на финансовых рынках.

· Анализ данных по рынку межбанковского кредитования РФ показывает, что соответствующие системные риски могут быть классифицированы как относящиеся к неперколятивной фазе.

· Для построения адекватной математической модели системных рисков, связанных с каскадными дефолтами, важно учитывать bow-tie структуру соответствующего ориентированного графа и его дисассортативность.

· Несмотря на то, что исходный граф характеризуется существенными отклонениями от древесной топологии, графы дефолтных каскадов являются древесными.