Методы оценки эффективности инновационных проектов с применением реальных опционов

Инновация по определению организации экономического развития и сотрудничества (ОЭСР) представляет собой введение в употребление какого-либо нового или значительно улучшенного продукта (товара, услуги) или процесса, нового метода маркетинга или нового организационного метода в управлении фирмой, организации труда или связях с общественностью.

Инновационная деятельность включает технологические, научные, финансовые, организационные и коммерческие действия, приводящие к реализации инноваций или осуществляемые с этой целью. Некоторые виды данного типа деятельности являются инновационными сами по себе, другие не обладают этим свойством, но тоже необходимы для осуществления инноваций. Инновационная деятельность включает также исследования и разработки, не связанные напрямую с подготовкой конкретной инновации [4].

Проблема оценки эффективности инновационных проектов

В связи с увеличением инновационной активности в России и мире все более актуальной становится проблема оценки экономической целесообразности инновационных проектов. Отличительной особенностью таких проектов является отсутствие рыночной статистики и данных, необходимых для определения параметров финансового моделирования, таких как емкость рынка, среднерыночная цена и другие параметры спроса. Это возникает вследствие отсутствия рынка на новый инновационный продукт, эффективность производства которого требует оценки. В данном случае под продуктом понимается как товар или услуга, так и предмет интеллектуальной собственности (к примеру, программное обеспечение).

Данный факт делает, с одной стороны, затруднительным прямой подсчет денежных потоков от проекта и расчет стандартных показателей, используемых при оценке инвестиционного проекта, таких как чистая приведенная стоимость, внутренняя норма доходности, индекс прибыльности, срок окупаемости. С другой стороны, данные показатели применительно к инновационному проекту становятся неинформативными из-за высокой степени неопределенности такого проекта.

Для инновационного проекта также характерна многостадийность. Как правило, он включает в себя такие этапы, как формирование идеи, научные исследования и разработки (R&D), внедрение продукта на рынок (коммерциализация), реализация продукта. При этом каждая стадия может завершиться как успехом, так и неудачей. Таким образом, переход на каждую последующую стадию проекта непосредственно связан с успехом предыдущей [3].

Построение дерева решений реализации инновационного проекта

Метод оценки инновационных проектов с применением реальных опционов позволяет учесть обе вышеперечисленные особенности. Он основан на учете управленческой гибкости в ходе реализации проекта, в отличие от традиционных методов оценки на базе чистой приведенной стоимости, предполагающих одновариантность развития проекта. Так, в ходе реализации проекта появляется информация, позволяющая менеджерам принять решение о прекращении проекта (например, если стадия исследований завершилась неудачей), об отсрочке реализации проекта (если начало стадии внедрения пришлось на экономический спад), или его расширении (в случае повышенного спроса). Данные возможности представляют собой реальные опционы, повышающие ценность проекта.

При оценке реальных опционов строится дерево решений (decision tree), узловыми точками в котором для инновационного проекта целесообразно выбрать границы стадий (конец одной – начало другой стадии).

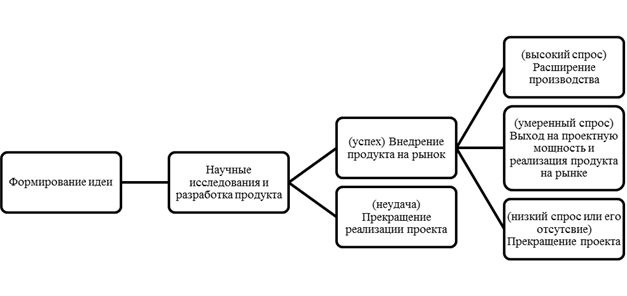
Рис. 1. Дерево решений реализации инновационного проекта

Инновационный проект, как показано на рисунке 1, представляет собой набор опционов, который по завершении каждой стадии предоставляет инвестору возможность инвестировать в следующий этап или отказаться от проекта, получив при этом ликвидационную стоимость, обычно меньшую первоначальных затрат. По мнению авторов, такой проект следовало бы оценивать нижеприведенным способом.

Оценка проектов с применением опционов

Предположим, что проект имеет 3 стадии (R&D, внедрение на рынок и работа на проектной мощности). Для начала разработок необходимо инвестировать , в случае неудачи (с вероятностью ) инициатор проекта получит ликвидационную стоимость с дисконтом , в случае успеха () – возможность инвестировать в дальнейшее развитие. На стадии внедрения продукта будут выявлены характеристики спроса, при низком спросе или его отсутствии (с вероятностью ) инициатор может отказаться от проекта, получив ликвидационную стоимость в размере. В случае умеренного или высокого спроса () инвестор получает возможность вложить , получив приведенную стоимость денежных потоков . Продолжительность стадии научных разработок составляет , стадии внедрения на рынок – лет. Дерево решений с платежами представлено на рисунке 2.

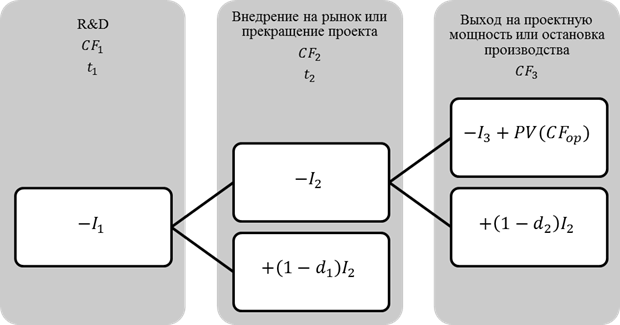
Рис. 2. Дерево решений инновационного проекта с платежами в узловых точках

Стоимость реального опциона call на внедрение продукта составит:

– приведенная стоимость денежных потоков проекта от операционной деятельности в случае успешного выхода продукта на рынок (денежных единиц);

– инвестиции во внедрение продукта на рынок (денежных единиц);

– дисконт инвестиционных затрат , с которым они могут быть реализованы;

– необходимые инвестиции для выхода на проектную мощность или расширения (денежных единиц).

Стоимость опциона call на научные разработки:

– дисконт инвестиционных затрат , . В большинстве случаев величина дисконта близка к 1, и инициатор теряет вложенные в разработки средства.

Критерием признания инновационного проекта эффективным в таком случае является . Данный критерий можно записать в более привычной форме , где выражение назовем модифицированным критерием NPV (MNPV).

Стоит учитывать, что использование предложенного критерия налагает некоторые ограничения на использование ставки дисконтирования () и вероятностей (). Предложенная модель требует использования в качестве ставки дисконтирования такую ставку, которая учитывает риск проекта, например, средневзвешенную стоимость капитала (WACC). Это, в свою очередь, предполагает использование объективных вероятностей в расчетах, в качестве которых могут выступать экспертные оценки возможностей развития событий (маркетинговые исследования), или модифицированные по количеству стадий вероятности, основанные на статистике Питера Боера [1], или вероятности, равные для каждого из исходов. При отсутствии объективной информации, основанной на исследованиях рынка или обработке статистических данных, принятие равновероятности исходов, по мнению авторов, является предпочтительным, поскольку соответствует максимальной энтропии (неопределенности), в условиях которой находится разработчик финансовой модели оценки проекта [2].

Приведенный метод описывает методику принятия решений относительно инвестирования в инновационный проект на основе цепочки реальных опционов. Кроме такого опциона на опцион при анализе проекта могут быть учтены другие реальные опционы, оценивающие возможность выхода из бизнеса, его расширения или тиражирования.

Модификация модели Блека-Шоулза

Принимая решение об инвестировании денежных средств в проект, инициатор условно приобретает опционы на перечисленные возможности, которые могут быть реализованы или нет в зависимости от развития проекта. Такие реальные опционы имеют прямую аналогию с финансовыми и оцениваются на основе тех же методов. Так, в случае реального опциона на отказ от бизнеса ценой исполнения выступает ликвидационная стоимость проекта, а текущей ценой актива – приведенная стоимость денежных потоков или стоимость фирмы. Такой опцион является опционом put и представляет собой возможность получения ликвидационной стоимости в случае неблагоприятного развития событий. Реальный опцион на расширение бизнеса является опционом call и представляет собой возможность получить дополнительную ценность (текущая цена опциона) в обмен на некоторый объем инвестиций (цена исполнения) в случае благоприятного развития событий, например, повышенного спроса.

Стоимость таких опционов может быть оценена с помощью двух методов: биномиального метода и на основе модели Блека-Шоулза. Первый предполагает построение бинарного дерева решений, в узловых точках которого будут находиться ожидаемые платежи при различных сценариях развития. Оценка данным методом аналогична вышеприведенному на основе критерия MNPV.

Метод оценки реальных опционов на основе модели Блека-Шоулза предполагает расчет по следующей формуле (для опциона call) [3]:

– цена исполнения опциона (денежных единиц);

– безрисковая ставка (% годовых);

– стандартное отклонение доходности базового актива (% годовых);

– время до исполнения опциона (лет);

– интегральная функция стандартного нормального распределения.

Модель (3) предполагает заранее известное стандартное отклонение (риск) реализации проекта, которое на практике заменяется стандартным отклонением доходности акций компании, реализующей проект [5]. Такая замена возможна только в случае, если компания оценивает эффективность проекта, который является копией данной компании с тем же уровнем риска. В другом случае в качестве стандартного отклонения используют среднеотраслевое значение, однако оно не отражает индивидуальный риск проекта и его возможности, которые оценивают с помощью реальных опционов. Для инновационного проекта подобные замены не могут быть использованы, поскольку, во-первых, данный проект не имеет действующих аналогов, во-вторых, в России нет информационно эффективного фондового рынка, который предоставлял бы данные, необходимые для расчета этого параметра.

Принимая во внимание вышесказанное, наиболее подходящим решением данной проблемы было бы определение параметров распределения денежных потоков от проекта (математического ожидания и стандартного отклонения) посредством имитационного моделирования (метод Монте-Карло). Данный способ предполагает генерирование большого количества сценариев развития событий на основе заданных распределений входных параметров финансовой модели. Имитационное моделирование в данном случае позволяет оценить неизвестный риск проекта на основе известных распределений экзогенных факторов, таких как уровень потребительских цен, уровень цен производителей, ставка кредитования и др., что представляется особенно актуальным в российских условиях.

Стандартная модель оценки опционов Блека-Шоулза неприменима к оценке реальных опционов на основе параметров, определенных в ходе имитационного моделирования, поскольку в известной модели используется стандартное отклонение доходностей базового актива в непрерывном виде, полученное в результате обработки исторических данных торгов, а не самого актива. Данное несоответствие параметров является критическим, однако в литературе игнорируется [5]. В этой связи авторами предлагается к использованию для оценки реальных опционов следующая модификация формулы Блека-Шоулза (для опциона CALL на расширение и тиражирование опыта):

– среднее значение и стандартное отклонение соответственно, где S – текущая стоимость денежных потоков проекта от операционной деятельности (денежных единиц);

k – коэффициент расширения (0<k<1) или тиражирования (k>1);

N – интегральная функция стандартного нормального распределения.

Предложенная модель оценки реальных опционов адаптирована под особенности получаемого в ходе имитационного моделирования распределения денежных потоков проекта. Модель (4) разработана на основе предположения о логнормальном распределении денежных потоков. Среднее значение и стандартное отклонение не имеют временной размерности, как в случае стандартной модели Блека-Шоулза, что устраняет несоответствие параметров. Величины S, X и C выражены в текущих ценах, что не требует учета временной стоимости денег. Вывод модели (4) был произведен авторами на основе предположения о справедливой стоимости опциона с применением интегрирования денежных потоков проекта по их вероятности, получаемой в результате имитационного моделирования. Стоимость опционов, рассчитанных по модели (4), добавляются к NPV проекта. В случае если сумма NPV и реальных опционов положительна, проект следует признать экономически эффективным.

Выводы

Разработанный алгоритм, а также представленная модель оценки стоимости реальных опционов могут быть использованы при принятии решений об инвестировании в какой-либо инновационный проект. Дальнейшие исследования предполагается направить на усовершенствование предложенных подходов, а также на их адаптацию к условиям российского рынка.