Modeling subscription service in the library

Введение

Системная картина мира предполагает, что при поиске оптимального состояния какой-либо системы необходимо использовать как можно более широкий арсенал методов различных научных направлений. Междисциплинарные научные исследования оказываются столь популярными, что уже, пожалуй, нет сферы, которой они не были бы охвачены [1].

Функционирование экономической системы общества и ее подсистем не стало исключением. На протяжении десятилетий активно развивается использование математических методов при анализе состояния и поведения экономических систем. Однако, к сожалению, когда речь заходит о прикладных аспектах экономической науки, например о сфере бухгалтерского учета или организации системы внутреннего документооборота в компании, то применение современного математического инструментария все еще ограничено [2].

Математические методы активно используются при анализе бухгалтерско-аналитической информации, обосновании теории бухгалтерского учета [3]. Однако библиотечная сфера всегда оказывалась в стороне от применения каких-либо математизированных подходов с использованием современных методов [4].

Заметим, что в современной математической науке существует достаточно большое количество ветвей методов, которые позиционируются, как математические и могут быть использованы при решении экономических задач. Это и теория игр, и большая часть направлений эконометрики, и положения теории массового обслуживания [5]. Изыскание возможности использования последней для оптимизации работы библиотеки и является объектом исследования в данной работе.

В ходе анализа эффективности деятельности библиотеки как учреждения важное место занимает метод математического моделирования, позволяющих наиболее оптимальным, точным и обоснованным способом оценить целесообразность принимаемых управленческих решений. Большое количество библиотечных процессов может быть сведено определенным системам, подающимся количественному описанию стандартными методами математического моделирования и системного анализа [6]. В качестве примера одного из таких библиотечных процессов, которые можно свести к функционированию широко распространённого вида систем, можно привести обслуживание читателей на абонементе. Абонементное обслуживание вполне адекватно представляется как работа так называемой системы массового обслуживания (СМО) [7].

Целью данной работы является построение модели библиотечного обслуживания читателей на абонементе в рамках теории систем массового обслуживания. Научная новизна работы заключается в построении модели абонементного обслуживания в библиотеке с применением теории систем массового обслуживания, а также в обосновании его экономической эффективности с целью оптимизации персонала.

Материалы и методы

Управление процессом абонементного обслуживания читателей в библиотеке ставит ряд важных практических задач, например таких, как оценка эффективности деятельности абонемента как отдела учреждения, которые можно решить с помощью теории СМО [8]. В данной теории система представляется в виде совокупности взаимосвязанных устройств, способных выполнять однотипные операции, и на них поступают требующие выполнения задания, для которых они предназначены [9].

Используются такие понятия: канал – это обслуживающее устройство, система массового обслуживания – это совокупность каналов, объединенных общей задачей, заявка – это объект, требующий обслуживания [10]. Предметом теории массового обслуживания является анализ зависимостей между характером потока заявок, производительностью отдельного канала, числом каналов и эффективностью обслуживания [11].

Обычно выделяются несколько видов СМО:

1) СМО с отказами – когда каждая пришедшая заявка, заставшая канал занятым, покидает систему не обслуженной.

2) СМО с ограниченной очередью – когда заявки покидают систему без обслуживания, если длина очереди превышает некоторое разумное (для сложившихся условий) значение.

3) СМО с неограниченной очередью – когда заявка будет всегда ожидать обслуживания вне зависимости от длины очереди [12].

Также выделяются два основных этапа функционирования СМО [13]:

1-й этап – это переходной процесс, определяемый начальными условиями: числом заявок в очереди на момент начала работы СМО. Этот процесс описывается системой дифференциальных уравнений относительно неизвестных и искомых в данной задаче функций р_n(t) – вероятностей того, что в момент времени в системе находится (на обслуживании и в очереди) заявок.

2-й этап – это стационарный режим, характеризуемый малым влиянием начальных условий. В этом случае р_n(t) – const и р¢_n(t). Подставляя в модель (систему дифференциальных уравнений) это значение, переходим к простому типу систем линейных алгебраических уравнений относительно постоянных и неизвестных р_n.

Чаще всего рассматривается простейшим поток заявок, который должен удовлетворять требованиям:

1) быть стационарным – это означает, что вероятность прихода некоторого числа событий за указанный промежуток времени должна зависеть от величины этого промежутка, но не зависеть от положения этого промежутка времени на оси t, то есть свойства потока не должны меняться с течением времени.

2) должно отсутствовать последействие, то есть для любых двух не перекрывающихся участков времени, числа событий на них не должны зависеть друг от друга.

3) быть ординарным – это означает, что вероятность попадания на элементарный участок времени Dt двух и более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Как известно, при выполнении данных требований, простейшим поток заявок как случайная величина подчиняется распределению Пуассона [14].

Результаты

В данной работе предлагается следующее построение модели библиотечного обслуживания читателей на абонементе. Работник библиотеки, обслуживающий читателя в зале абонемента, в контексте теории СМО является устройством. Приходящие в случайные моменты времени на абонементное обслуживание читатели являются объектами, требующие выполнения от библиотекаря (устройства) выполнения определенной операции [15]. Если в момент прихода читателя библиотекарь в абонементном зале свободен, то он принимается на обслуживание, то есть читатель сразу же обслуживается и задача отдела считается успешно выполненной, так как читатель покинет его обслуженным. Если же библиотекарь занят обслуживанием другого читателя, то вновь пришедший читатель, в зависимости от принятой формы обслуживания, либо становится в очередь либо покидает абонемент необслуженным.

Исходные параметры модели абонементного обслуживания как СМО:

n – число библиотекарей, занятых на абонентном обслуживании в данной библиотеке;

l – среднее число читателей, приходящих на абонентное обслуживание в единицу времени, которая называется интенсивностью потока читателей;

– среднее время обслуживания читателя на абонементе;

α – условная доходность от обслуживания одного читателя – характеристика качества обслуживания читателя, приносящее выгоду библиотеке, поднятие ее рейтинга и статуса, обеспечивающее, ее в конечном итоге, более выгодным финансированием (определяется на основе статистической отчетности библиотеки по показателям эффективности библиотечного обслуживания);

Основные характеристики эффективности обслуживания читателей на абонементе:

А – среднее число читателей, обслуживаемых на абонементе в единицу времени, которая называется абсолютной пропускной способностью абонемента;

Q – вероятность обслуживания читателя по очереди, которая называется относительной пропускной способностью абонемента:

Q=A/l; (1)

P – вероятность отказа, то есть вероятность того, что пришедший в абонемент читатель не будет обслужен:

P=1–Q; (2)

z – среднее число читателей, находящихся в зале абонемента, то есть тех, которые либо обслуживаются, либо ожидают в очереди;

r – среднее число читателей, ожидающих в очереди обслуживания;

T_a – среднее время нахождения читателя в зале абонемента, то есть среднее время, затрачиваемое им на ожидание в очереди и обслуживание (формула Литтла):

T_a=z/l; (3)

T_о – среднее время ожидания в очереди:

T_о=r/l; (4)

N_b – среднее число занятых на абонентном обслуживании библиотекарей:

; (5)

D – условная доходность от обслуживания всех читателей в единицу времени: D=α×A.

Моделирование абонементного обслуживания, осуществляемого n библиотекарями, когда в случае занятости всех библиотекарей читатели уходят и не ждут обслуживания, то есть они в очередь не становятся, основано на формулах Эрланга для многоканальной СМО с отказами:

1) вероятность того, что все библиотекари на абонементе свободны:

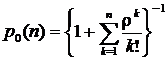, (6)

2) вероятность того, что k библиотекарей на абонементе заняты:

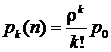, k=1, 2 ,…, n, (7)

где .

Показатели эффективности в данной модели:

Q=1-p_n(n); P=p_n(n); A=l×(1-p_n(n)); N_b=r×(1-p_n(n)). (8)

Моделирование абонементного обслуживания, осуществляемого n библиотекарями, когда в случае занятости всех библиотекарей читатели становятся в очередь, которая имеет ограниченное количество m мест, основано на формулах для многоканальной СМО с ограниченной по длине очередью:

1) вероятность того, что все библиотекари на абонементе свободны:

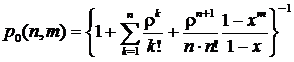, если x=r/n¹1 или (9)

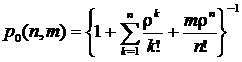, если x=r/n=1; (10)

2) вероятность того, что k библиотекарей на абонементе заняты:

, k=1, 2 ,…, n; (11)

3) вероятность того, что k библиотекарей на абонементе заняты и в очереди j читателей:

, j=1, 2 ,…, m, если x¹1 или (12)

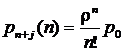, j=1, 2 ,…, m, если x=1. (13)

Показатели эффективности в данной модели:

Q=1-p_n+j; P=p_n+j; A=l×(1-p_n+j); N_b=r×(1-p_n+j); z=r+N_b; (14)

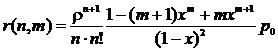, если x¹1 или (15)

, если x=1. (16)

Обсуждение

В качестве примера использования математического аппарата теории СМО в моделировании библиотечных процессов проведем анализ эффективности абонементного обслуживания с целью оценки экономической целесообразности увеличения количества работающих на нем библиотекарей. Положим, что на абонементном обслуживании в зале заняты два библиотекаря, которые могут обслуживать двух читателей. Будем считать, что если библиотекари заняты, то читатели в очередь не становятся и уходят. По результатам анализа статистической отчетности установлено, что среднее число читателей, приходящих на абонентное обслуживание в единицу времени, то есть интенсивность потока читателей, составляет 4 читателя в час, а среднее время обслуживания одного читателя равно 0,8 часа. Содержание каждого библиотекаря, занятого на абонементном обслуживании, обходится библиотеке в 200 рублей за час работы. Условная доходность от обслуживания одного читателя составляет 400 рублей. Таким образом, в обозначениях принятой модели многоканальной СМО с отказами будет:

n=2, , l=4, α=400, тогда r=3,2.

Далее, по формулам Эрланга (6) и (7) вычисляются величины:

p₀(2)=0,107; p₂(2)=P=0,549.

Затем рассчитываются показатели эффективности (8):

Q(2)=0,451; A(2)=1,803 заявки в час.

Условная доходность от обслуживания всех читателей:

D(2)=α×A(2)=721,03 рубля в час.

Пусть теперь при тех же условиях на абонементном обслуживании работаю три библиотекаря. Тогда n=3, и по формулам (6)-(8) получается:

p₀(3)=0,068; p₃(3)=P=0,369; Q(3)=0,631; A(3)=2,522 заявки в час;

Теперь условная доходность от обслуживания всех читателей:

D(3)=α×A(3)=1008,84 рубля в час.

Увеличение условной доходности составляет

DD=D(3)-D(2)=287,81 рубля в час.

Теперь данное значение следует сравнить с увеличением расходов на включение в абонементное обслуживание еще одно библиотекаря, которое составляет 200 рублей в час. Видно, что при таких условиях экономически целесообразно увеличение на одно рабочее место в абонементе. Положительный экономический эффект равен 87, 81 рублей в час, что составляет 43,9% от затрат на содержания одного библиотекаря.

В качестве другого примера использования математического аппарата теории СМО в моделировании библиотечных процессов проведем анализ эффективности абонементного обслуживания с целью оценки целесообразности увеличения количества мест ожидания для читателей, пришедших в зал абонементного обслуживания. Также как и в предыдущем примере, пусть на абонементном обслуживании в зале заняты два библиотекаря, которые могут обслуживать читателей. По результатам анализа статистической отчетности установлено, что среднее число читателей, приходящих на абонентное обслуживание в единицу времени, то есть интенсивность потока читателей, составляет 1 читатель в минуту, а среднее время обслуживания одного читателя равно 2 минуты. Теперь пусть моделируемая ситуация меняется теперь в том плане, что читатели могут оставаться в зале, ожидая в очереди своего обслуживания. Однако, максимальное число мест в очереди лимитировано, например, количеством комфортных сидячих мест ожидания. Другими словами, в очереди в абонементном зале могут находиться не более определенного числа m читателей. Требуется оценить, стоит ли увеличивать максимальное количество таких мест ожидания с четырех до пяти.

Таким образом, в обозначениях для модели многоканальной СМО с ограниченной по длине очередью будет:

n=2, , l=1, тогда r=2.

Так как для таких значений исходных данных x=r/n=1, то по формулам (10), (11) и (13) находятся вероятности сначала для m=4:

p₀(2, 4)=1/13; p₁(2)=p₂(2)=p₃(2)=p₄(2)=p₅(2)=p₆(2)=2/13.

Отсюда показатели эффективности (14) обслуживания читателей при ограничении в очереди из 4-х мест:

Q(4)=11/13; A(4)=11/13 заявки в минуту.

Теперь следует по формулам (10), (11) и (13) определить значения вероятностей для m=5:

p₀(2, 5)=1/15; p₁(2)=p₂(2)=p₃(2)=p₄(2)=p₅(2)=p₆(2)=p₇(2)=2/15.

Отсюда показатели эффективности обслуживания читателей при ограничении в очереди из 5-х мест:

Q(5)=13/15; A(5)=13/15 заявки в минуту.

Для оценки целесообразности увеличения максимального числа мест ожидания с четырех до пяти следует сравнить значения среднего числа читателей, обслуживаемых на абонементе в единицу времени, то есть абсолютной пропускной способности абонемента, для случаев ограничений максимального числа в очереди для 4-х и 5-и мест. Прирост абсолютной пропускной способности абонемента A(5)-A(4)=0,021 заявки в минуту. Более информативным, с точки зрения анализа эффективности обслуживания читателей, является относительный прирост абсолютной пропускной способности абонемента, который в рассматриваемом примере составляет всего 2,42% от исходного значения ограничения максимального числа мест в очереди. На основании этого можно вполне обосновано утверждать, что расширение «зала ожидания», то есть увеличение максимального числа мест ожидания с 4-х до 5-и мест при данных условиях не целесообразно, так как оно очень слабо влияет на эффективность работы абонемента в целом.

Заключение

В данной работе построена математическая модель абонементного обслуживания с использованием теории систем массового обслуживания. На ее основе проведен анализ эффективности абонементного обслуживания с целью оценки экономической целесообразности оптимизации количества работающих на нем библиотекарей. В качестве примера использования сформулированной модели показано, что если на абонементном обслуживании в зале заняты два библиотекаря, то целесообразно увеличить на одно рабочее место в абонементе. Также показано, что увеличение числа мест ожидания читателей в зале на одно при данных условиях практически не влияет на эффективность работы абонемента в целом. Оценена величина положительного экономического эффекта таких управленческих решений.

Следует отметить, что при моделировании в данной работе не учитывается возможность самостоятельного принятия читателем решения в любой момент времени об отказе ожидать обслуживания на абонементе по различным субъективным причинам, в том числе, при наличии большой, по его мнению, очереди, предполагающей длительного времени ожидания.